A hô kinetikus elmélete: az elsô lépések
A hôszubsztancia-elmélet ... elérte teljesítôképességének határát. A XIX. század elsô felében a hôtani vizsgálatokhoz ugyan még mindig ez szolgáltatta a hátteret, de legeredményesebb hívei, így CARNOT és LAPLACE is, felvetették azt a lehetôséget, hogy a hô mégiscsak az anyagi részecskék mozgása. A nehézség csak az volt, hogy ezzel az elképzeléssel nem tudtak kvantitatív törvényekhez eljutni.
A kinetikus elmélet – mint azt már említettük – régi keletû. Már BACON határozottan kijelentette, hogy a hô és a mozgás között szoros kapcsolat áll fenn. Az egész XVII. század ezt a felfogást vallotta magáénak. Az elmélet kvantitatív kidolgozása azonban csak a "bázeliek" munkásságával kezdôdött. JAKOB HERMANN (1678–1733) 1716-ban minden indokolás nélkül ugyan, de már megállapítj a, hogy a hô a 'test sûrûségével és a mozgás négyzetével arányos'. EULER, mint annyi más téren, itt is úttörô munkát végzett: eljut a részecskesebesség számszerû értékéhez is: v ~ 477 ms–1. 1738-ban DANIEL BERNOULLI hidrodinamikájában már a mai elemi kinetikus gázelmélethez nagyon hasonló elképzeléssel a
összefüggést vezeti le. BERRNULLI úgy képzeli, hogy az egyenes vonalban ide-oda száguldó részecskék ütközése az, ami végül is a nyomást létrehozza. Amint az ábrából látni lehet, az anyag részeit BERNOULLI nem egyformának és nem szabályos alakúnak tételezi fel. BERNOULLI kvantitatív megfontolásai egyelôre nem találnak visszhangra; közel száz évre feledésbe merülnek. Elôször újra JOHN HERAPATHnál találkozunk BERNOULLI eszméivel 1816-ban; HERAPATH (1790– 1868) nem lépett elôre; sôt, a hômérsékletet – helytelenül, és BERNOULLIval ellentétben – a részecskék impulzusával hozta kapcsolatba. Így ellenfeleinek, akik között olyan tekintély is volt, mint DAVY, nem okozott különösebb nehézséget, hogy elhallgattassák.p ~ nmv2
Lényeges elôrehaladást jelentett JoHN JAMES WATERSTON (1811–1883) elmélete, amelyet a negyvenes évek elején dolgozott ki. WATERSTON munkásságának sorsa igen tanulságos. Mint a fizikában ismeretlen kezdô, Bombayból küldte be munkáját a Royal Societynak. A cikket véleményezés végett kiadták két elismert szakembernek. A két véleményezô közül csak az egyik talált némileg elismerô szavakat az egyébként elutasító vélemény mellett. A másik azonban egyszerûen teljes értelmetlenségnek tartotta az egész dolgozatot.
WATERSTON munkája és személye is végleg a feledés homályába merült volna, ha egyrészt nem sikerül neki mégiscsak megjelentetni egy rövid kivonatot gondolatairól, másrészt ha a Royal Society irattárában 1891-ben LORD RAYLEIGH fel nem fedezte volna az eredeti kéziratot. Ilyen módon félévszázados késéssel WATERSTON cikke mégiscsak megjelent a Royal Society lapjában. Ezzel kapcsolatban még külön figyelemre méltó LORD RAYLEIGH tanácsa a fiatal fizikusok számára, hogy elkerüljék a hasonló sorsot: túlságosan eredeti gondolatokat tartalmazó cikkeiket ne egy tudós társaságnak küldjék be, és különben is jobb, ha elôbb valamilyen elfogadott témakörben könnyen megítélhetô gondolatokkal vívják ki az elismerést. És mindezt LORD RAYLEIGH teljesen komolyan gondolta...
A szerzô a gázok tulajdonságait, már ami a hôt és a rugalmasságot illeti, egy különös elméletbôl vezeti le, amely a hôt úgy tekinti, mint ami az anyag részecskéinek kicsi, de nagyon gyors mozgásából áll. Úgy képzeli, hogy a gáz atomjai, amelyek teljesen elasztikusak, állandó mozgásban vannak minden irányban, és azáltal vannak egy határolt térrészbe kényszerítve, hogy egymással, illetve a környezô testek részecskéivel ütköznek. Ezen mozgások eleven ereje a gáz egy meghatározott részében jelenti a hôt, amely ebben a részben van.Megmutatja, hogy ez a mozgásállapot a gáznak egy, a molekuláris mozgássebesség négyzetének közepével, valamint az atomok egységnyi térfogatban vett tömegével – más szóval az anyag sûrûségével – arányos rugalmasságot ad. Ez a rugalmasság egy adott gázban a hômérséklet mértéke.
Két gáz között az egyensúly akkor áll be, ha az egységnyi térfogatban az atomok száma azonos, és minden egyes atom eleven ereje is egyforma. A hômérséklet tehát minden gázban arányos az egy atom tömegével szorozva a molekuláris mozgás sebességének négyzetes közepével, ha a hômérsékletet egy abszolút nullától mérjük, amely a Fahrenheit-hômérô nullája alatt 49o-kal van. (Ez valószínû sajtóhiba 461o helyett.)
Ha a gázt összenyomjuk, az összenyomásra szánt mechanikai munka átadódik a molekuláknak, hogy megnövelje azok eleven erejét; és fordítva, ha a gáz kiterjed, a mechanikai munkát az eleven erô rovására kapjuk.
J. J. WATERSTON, On a General Theory of Gases. Rep. Brit. Assn. Adv. Sc. 1851
A [fenti] idézetben WATERSTON elméletét összefoglaló
cikkét láthatjuk – majdnem teljes terjedelmében. A
szerzô "különös elmélete" teljesen modern hangvételû.
WATERSTON legfontosabb eredményének azt tekinthetjük,
hogy az elôzô kinetikus elméletek által elért
eredményeket is pontosabban fogalmazza meg. Ezeken túlmenôen
ô fogalmazta meg elôször az energiaekvipartició-elv
egy speciális esetét: a hômérsékleti
egyensúlyban levô két gáz minden atomjának
közepes kinetikus energiája azonos. Az ekvipartició
elvének szerepérôl a klasszikus statisztikus elméletben
a késôbbiekben még szó lesz. Itt csak annyit
kívánunk megjegyezni, hogy most találjuk meg elôször
a feleletet BLACKnek arra a kérdésére, hogy miért
nem következik szükségszerûen a kinetikus elméletbôl
a fajhô és a test sûrûségének arányossága.
Mindezek után érthetô, hogy WATERSTON semmilyen
hatással nem volt a kinetikus elmélet továbbfejlôdésére;
a folytatás, vagy helyesebben újrakezdés folyamata
egy évtized múlva – kissé alacsonyabb színvonalról
indulva, mint WATERSTONé – nem Angliában, hanem Németországban
indult meg.
Az energiamegmaradás tétele
Közben azonban a negyvenes évek elején megérett az idô arra, hogy az energiamegmaradás tételét megfogalmazhassák.
Az energiamegmaradás tételének fejfedezését három névhez szokás kapcsolni: JULIUS ROBERT MAYER, (1814–1878), JAMES PRESCOTT JOULE (1818–1889) és HERMANN VON HELMHOLTZ (1821–1894). Hozzá kell tennünk azonban, hogy hasonló gondolat számtalan kutató fejében megfordult. Így a kémia és hôenergia kapcsolatát, az életjelenségek energetikai oldalát JUSTUS LIEBIG fejtette ki.
ROBERT MAYER figyelmét is egy ilyen jelenség hívta
fel: mint hajóorvos észrevette, hogy a trópusokon
a matrózok vénás vére pirosabb, mint zordabb
idôjárású születési helyükön
lenni szokott. Ebbôl helyesen arra következtetett, hogy a szervezetben
ilyenkor kisebb fokú oxidációs folyamatok zajlanak
le, minthogy az életmûködéshez szükséges
hô egy részét a természet szolgáltatja.
1842ben megjelent Bemerkungen über die Kräfte der unbelebten
Natur címû munkája igen erôsen magán
viseli a Naturphilosophie bélyegét, és így
nem csoda, ha az akkori idôk vezetô fizikai folyóirata,
az Annalen der Physik nem volt hajlandó közölni.
Végül is LIEBIG helyezte el a cikket egy kémiai folyóiratban.
A cikk bevezetô részeit olvasva megértjük a fizikusok
viszolygását egy olyan munkától, amely minden
állítását a
"Causa aequat effectum", vagyis
az ok egyenlô az okozattal alaptételbôl vezeti Ie. Vagy
figyeljük meg azt az okoskodását, amellyel plauzibilissé
akarja tenni, hogy a leesô test végül is a hômérsékletet
növeli. Abból indul ugyanis ki, hogy a testek összenyomásakor,
vagyis térfogatcsökkenésekor a tapasztalat szerint hô
fejlôdik. Egy, a magasból leesô kôdarab pedig
a Föld felszínéhez közeledve a Földnek mint
egésznek a térfogatát csökkenti: ehhez a térfogathoz
eddig hozzátartozott a magasban levô kôdarab is. Ezért
növekszik meg tehát a hômérséklet...
... Az erôk okok, és így azokra teljes mértékben alkalmazható az alaptétel: causa aequat effectum. Ha a c ok okozata e, akkor c = e; ha e ismét az oka egy másik f okozatnak, akkor e = f stb. c = e = f . . . = c. Az okok és okozatok egy láncolatában, mint ahogy az egy egyenlet természetétôl következik, sohasem válhat egy tag vagy egy tag egy része nullává. Minden ok elsô tulajdonsága tehát az elpusztíthatatlansága.Szinte meglepetésként éri az olvasót a cikk befejezése, ahol teljesen helyesen veti fel a kérdést, hogy egy meghatározott magasságból esô test hômérséklete leesésekor egészen meghatározott értékkel kell hogy emelkedjék. Mint kérdést veti fel, hogy milyen magasból kellene egy testet leejteni ahhoz, hogy hômérséklete éppen egy fokkal emelkedjék. A kísérletet ROBERT MAYER természetesen nem végezte el, ennek ellenére felel a kérdésre: a gázok állandó térfogaton és állandó nyomáson vett fajhôjének viszonyából következtet a hô munkaegyenértékére. A számérték (~360 mkp) ugyan erôsen eltér a JOULE által megmért és ma is érvényesnek tartott 425 mkp értéktôl, de a nagyságrend és az elv teljesen helyes.Ha az adott c ok létrehozta a vele egyenlô e hatást, ezzel c egyúttal megszûnt létezni; c tehát e-vé vált; ha e létrehozása után c egészen vagy részben még megmaradt volna, úgy ezen visszamaradó oknak további okozat kellene hogy megfeleljen; c okozata tehát e kellene hogy legyen ellentétben c = e feltevésünkkel. Így, minthogy c e-be, e f-be stb. megy át, ezeket a mennyiségeket egy és ugyanazon objektum különbözô megjelenési formáinak kell tekintenünk. Az a képesség, hogy különbözô formákat tud felvenni, a másik lényeges tulajdonsága minden oknak. A két tulajdonságot összefoglalva mondhatjuk: az okok kvantitatíve elpusztíthatatlanok és kvalitatíve változékony objektumok.
A természetben az okok két nagy osztálya létezik, amelyek között a tapasztalat szerint nincs átmenet. Az egyik osztályt azok az okok alkotják, amelyek ponderábilisak és inpenetrábilisak: az anyagok; a másik osztályt azok az okok teszik ki, amelyeknél hiányoznak ezek a tulajdonságok: az erôk ... Az erôk tehát: elpusztíthatatlan, változékony, imponderábilis objektumok.
... ha az ok az anyag, akkor az okozat is anyag; ha az ok erô, az okozat is erô ...
Az esési erô, mozgás és hô között fennálló természetes összefüggést az alábbi módon tehetjük szemléletessé: Tudjuk, hogy a hô úgy lép elôtérbe, hogy a test egyes anyagrészei egymáshoz közelebb igyekeznek; az összenyomás hôt fejleszt; ami most már a legkisebb anyagrészekre és a köztük levô legkisebb térre igaz, alkalmazható kell hogy legyen nagy tömegekre és mérhetô térrészekre is. Egy teher süllyesztése a Föld számára tényleges térfogatcsökkenést jelent, minden bizonnyal kapcsolatban kell hogy álljon az ilyenkor fellépô hôvel; ennek a hônek a teher nagyságával és a távolságával pontosan arányosnak kell lennie ...
Téziseinket, amelyek szükségszerûen következnek a "causa aequat effectum" alaptételbôl, és amelyek tökéletes összhangban állnak az összes természeti jelenséggel, egy gyakorlati következtetéssel zárjuk ... meg kell határoznunk, hogy milyen magasra kell a Föld felszíne fölé emelni egy meghatározott súlyt, hogy az esési ereje ekvivalens legyen az azonos súlyú vízmennyiség 0-ról 1 oC-ra való melegítésével. Hogy egy ilyen egyenlet a természetben gyökerezik, tekinthetô az eddigiek rezüméjének.
A gázokra vonatkozó ismert hô- és térfogatviszonyok alkalmazásából ..., az atmoszferikus levegô állandó nyomáson és állandó térfogaton mért kapacitásának hányadát 1,421-nek véve, az adódik, hogy egy súly lesüllyedése kb. 365 m magasságból megfelel egy hasonló súlyú víz 0-ról 1 oC-ra való melegedésének.
ROBERT MAYER: Bemerkungen über die Kräfte der unbelebten Natur
JOULE már 1841-ben közzétette az áram hôhatására vonatkozó és róla elnevezett törvényt, amely szerint egy ellenálláson az áram hatására keltett hô egyenesen arányos az áramerôsség négyzetével, az ellenállással és az idôvel:
Az energiamegmaradás tételével kapcsolatos alapvetô munkája 1845-ben jelent meg On the Existence of an Equivalent Relation between Heat and the Ordinary Forms of Mechanical Power címen. A mérés elve és a berendezés a mai középiskolai fizika tananyagához tartozik. Egy meghatározott súlyú test potenciális energiáját egy lapátos folyadékkeverôben hôenergiává alakítjuk. A mérés pontos elvégzése természetesen igen nagy gondosságot igényel. JOULE elsô mérései nem szolgáltatták a helyes, ma is elfogadott értéket, viszont módszerét egyre finomította, a hibaforrásokat kiküszöbölte, vagy befolyásukat figyelembe vette, és így jutott el a hô mechanikai egyenértékének ma is elfogadott értékéhez, pontosabban egy ahhoz igen közel esô értékhez: 1 kcal ~ 424 mkp.Q~ I2Rt.
HELMHOLTZ ide vonatkozó munkája 1847-ben jelent meg: Über die Erhaltung der Kraft címmel. Jóllehet HELMHOLTZ stílusán is megérzôdik a romantikus természetfilozófia hatása, de tárgyalásmódja már teljesen a ma fizikusának szája íze szerint való.
Az energiamegmaradás tételének fontossága
miatt érdemes megvizsgálni, hogyan látták azt
maguk a fôszereplôk, és itt elsôsorban a józan,
reális, az angol empirista hagyományokon nevelt JOULE-ra
gondolunk. Az 1850-ben írt visszaemlékezésébôl
megtudhatjuk, hogy JOULE maga is érettnek látta már
az idôt arra, hogy az energiamegmaradás tétele megfogalmazódjék.
Ennek ellenére a tudományos közvélemény
igen nehezen fogadta el. JOULE elsô bejelentése teljes közönybe
fulladt volna, ha egyetlenegy ember nem figyel fel rá, és
hitetlenkedve ugyan, de megsejti
a felfedezés fontosságát. Ez a lelkesedô fiatalember
WILLIAM THOMSON, a késôbbi LORD KELVIN.
A kinetikus gázelmélet
Az energiamegmaradás elvének megfogalmazásával az anyag kinetikus elmélete – egyelôre a kinetikus gázelmélet – újból érdekessé vált; pontosabban újra felfedezték, és most már semmi akadálya sem volt az elismertetésének. Maga JOULE már 1848-ban – HERAPATHra hivatkozva – megkísérelte kiszámítani a hidrogénmolekula sebességét és az állandó térfogaton mért fajhôt. Munkája 1851-ben jelent meg, anélkül hogy különösebb feltûnést keltett volna.
Az áttörés ezen a vonalon AUGUST KARL KRÖNIG (1822–1879) érdeme, akinek 1856-ban megjelent rövid cikke tartalmilag nem jelenetett ugyan elôrelépést, de az erre megérett idôben egy elismert professzor kellô súlyával tett kijelentései kiváltó okként hatottak. Ettôl kezdve a makroszkopikus termodinamika és a kinetikus gázelmélet, illetve klasszikus statisztika egymást kiegészítve haladt elôre olyan emberek közremûködésével, mint RUDOLF CLAUSIUS, J. C. MAXWELL, WILLIAM THOMSON, LUDWIG BOLTZMANN, hogy csak a legfontosabb neveket említsük.
Az alapozás – mind a makro, mind a mikro vonalon – CLAUSIUS érdeme. "Über die Art der Bewegung, welche wir Wärme nennen" címû, 1857-ben az Annalen der Physikben megjelent cikkében az elméleti fizikakönyvekben ma is szokásos módon vezeti le az állapotegyenletet
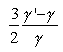
CLAUSIUS vezette be a szabad úthossz fogalmát is, és vette el az élét mindazon ellenvetéseknek, amelyek a gázrészecskék óriási sebessége (hidrogén esetében 1800 m/s) és a lassú diffúziója közötti látszólagos ellentmondást hangsúlyozták.
MAXWELL a kinetikus gázelmélettel való foglalkozást úgy fogta fel, mint érdekes "gyakorló feladatot a mechanikában". Teljesen függetlenül a gázok kinetikus elméletétôl, érdemes megvizsgálni – írja egyik levelében MAXWELL –, hogyan viselkedik a rugalmas golyók igen nagyszámú egyedbôl álló halmaza, ha azok csak az ütközésen keresztül hathatnak egymásra. 1860-ban megjelent munkájának legfôbb eredménye a ma is az ô nevét viselô sebességeloszlási függvény meghatározása. Ezek szerint azon részecskék száma, amelyek sebessége a v és v+dv sebesség intervallumba esik
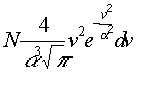
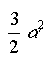
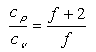
kapcsolatot MAXWELL 1866-ban találta meg (f itt a szabadsági fokok számát jelenti).