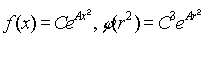
Illusztrációk a gázok dinamikus
elméletéhez
Részletek
Philosophical Magazine, Series 4, Vol. 19. p. 19, 1860
(in: William Francis Magie: A Source Book in Physics, Harvard University Press, Cambridge, Massachusetts, 1963)
Az anyagok – és különösen a gáz halmazállapotú anyagok – számos tulajdonsága levezethetõ abból a hipotézisbõl, hogy részecskéik gyors mozgást végeznek és a sebesség növekszik a hõmérséklet függvényében. Ennek a mozgásnak a pontos mibenléte érdekes vizsgálódás tárgya. Daniel Bernoulli, Herapath, Joule, Krönig, Clausius stb. megmutatta, hogy a tökéletes gázok nyomása, hõmérséklete és sûrûsége megmagyarázható azzal a feltevéssel, hogy a részecskék egyenletes sebességû, egyenes vonalú mozgást végeznek, a tartály falainak ütköznek, s így nyomást hoznak létre. Nem szükséges feltenni, hogy az egyes részecskék nagy távolságra jussanak ugyanazon az egyenes vonalon, mert a nyomás akkor is fellép, ha a részecskék egymással ütköznek, ezért az említett egyenes vonal igen rövid lehet. Clausius úr meghatározta a részecskék átlagos úthosszát és két részecske középpontjának távolságát az ütközés létrejöttekor. Jelenleg nem rendelkezünk olyan eszközzel, amellyel ezeket a távolságokat igazolhatnánk, de van néhány jelenség, például a gázok belsõ súrlódása, a gázok hõvezetése és a gázok más gázokban zajló diffúziója, amely lehetõséget adhat a részecskék sorozatos ütközései között kialakuló átlagos úthossz pontos meghatározására. Hogy ezeket a vizsgálatokat szilárd mechanikai elvekre helyezzük, megadom a végtelen számú, kis, kemény és tökéletesen rugalmas, csak ütközés során kölcsönható gömb mozgástörvényeit.
Ha ennek a rendszernek a tulajdonságai megegyeznek a gázok tulajdonságaival, fontos fizikai analógia állítható fel, amely az anyag tulajdonságainak pontosabb ismeretéhez vezethet. Ha a gázokkal végzett kísérletek inkonzisztensek a javasolt hipotézissel, akkor elméletünk – bár önmagában konzisztens – alkalmatlannak bizonyul a gázok jelenségeinek magyarázatára. Minkét esetben le kell vonnunk a hipotézis következményeit..
Ahelyett, hogy a részecskéket keménynek, gömb alakúnak és rugalmasnak tekintjük, azt is mondhatjuk, hogy a részecskék olyan erõ középpontjai, amelynek hatása csak nagyon kis távolságon érzékelhetõ, ha hirtelen igen nagy intenizitású taszítóerõként jelenik meg. Nyilvánvaló, hogy mindkét feltevés ugyanazokhoz az eredményekhez vezet. A továbbiakban a tökéletesen rugalmas testek feltevését fogom követni, hogy elkerüljem eme taszítóerõk hosszas leírásának ismételgetését. Ha feltesszük, hogy az együtt mozgó molekula-együttesek határoló felülete nem gömb alakú, akkor – amint Clausius kimutatta – a rendszer forgó mozgása tárolja az eleven erõ bizonyos hányadát, s ezzel indokolhatjuk, hogy a fajhõ értéke nagyobb, mint ami az egyszerûbb hipotézis alapján adódik.
...
IV. Meghatározandó azoknak a részecskéknek az átlagos száma, amelyek sebessége adott határok közé esik nagyszámú egyenlõ részecske között lezajló nagyszámú ütközés után.
Legyen N a részecskék teljes száma. Legyen x, y, z az egyes részecskék sebességkomponense három egymásra merõleges irányban, valamint legyen az x és x + dx közötti részecskék száma Nf(x)dx, ahol az x-tõl függõ f(x) meghatározandó.
Az y és y + dy közötti részecskék száma Nf(y)dy, a z és z + dz közötti részecskék száma Nf(z)dz, ahol f mindig ugyanazt a függvényt jelenti.
Az x sebesség semmilyen módon nem befolyásolja az y vagy a z sebességet, mert ezek mind merõlegesek egymásra és függetlenek. Ezért azoknak a részecskéknek a száma, amelyek sebessége x és x + dx közé, illetve y és y + dy és z és z + dz közé esik:
Nf(x)f(y)f(z)dxdydz.
Ha feltesszük, hogy ugyanabban a pillanatban N részecske indul ki a kezdõpontból, akkor egységnyi idõ elteltével ennyi részecske lesz a (dxdydz) térfogatban, egységnyi térfogatban pedig
Nf(x)f(y)f(z)
lesz a számuk. De a koordináták iránya teljesen önkényes, ezért ennek a számnak csak a kezdõponttól vett távolságtól kell függnie, tehát
f(x)f(y)f(z) = f(x2 + y2 + z2).
Az egyenlet megoldásából azt kapjuk, hogy
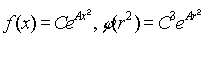
Ha A-t pozitívnak tekintjük, a részecskék száma nõni fog a sebesség függvényében, és a részecskék száma végtelenné válik. Ezért A-t negatívnak és –1/a2-nek tekintjük, tehát az x és x + dx közötti részecskék száma
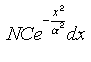
Ha x = – végtelen és x = + végtelen között integrálunk, megkapjuk a részecskék teljes számát:
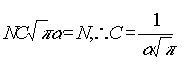
ezért f(x)
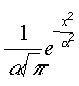
Ebbõl az alábbi következtetéseket vonhatjuk le.
Elõször. Azoknak a részecskéknek a száma,
amelyek sebessége – egy adott irányban – x és
x
+ dx közé esik,
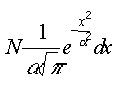 |
(1) |
Másodszor. Azoknak a részecskéknek a száma,
amelyek aktuális sebessége v és v +
dv
közé esik,
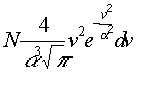 |
(2) |
Harmadszor. A v átlagának meghatározásához
adjuk össze mindegyik részecske sebességét, és
osszuk el a részecskék számával. Az eredmény:
| átlagsebesség = |
(3) |
Negyedszer. A v2 átlagának meghatározásához
adjuk össze mindegyik értéket, és osszuk el N-nel:
v2 átlagértéke = 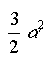 |
(4) |
Amint lennie kell, ez nagyobb, mint az átlagos sebesség négyzete.
Tehát a sebességek a részecskék között ugyanolyan törvény szerint oszlanak el, mint a hibák az észlelt adatok között a "legkisebb négyzetek módszerének" elméletében. A sebességek nulla és végtelen között változnak, de a nagy sebességgel rendelkezõ részecskék száma kicsi. Ezeken a minden irányban azonos sebességeken kívül a részecskék teljes rendszere általános haladó mozgást is végezhet, amelyet a részecskék egymáshoz viszonyított mozgásában figyelembe kell venni. Az egyiket haladó mozgásnak, a másikat keveredõ mozgásnak nevezhetjük.
| Vissza | http://www.kfki.hu/chemonet/
http://www.ch.bme.hu/chemonet/ |