Daniel Bernoulli
(1700–1782)
Hidrodinamika
1738
Részlet
(in: William Francis Magie: A Source Book in Physics, Harvard
University Press, Cambridge, Massachusetts, 1963)
 1.
Az elasztikus fluidumokhoz olyan szerkezetet rendelhetünk, amely összhangban
van összes ismert tulajdonságukkal, s így olyan tulajdonságaikat
is megvizsgálhatjuk, amelyeket még nem tanulmányoztunk
elegendõen. Az elasztikus fluidumok tulajdonságai a következõk:
1. nehezek; 2. minden irányban kiterjednek, ha szabadon mozoghatnak;
3. folyamatosan egyre jobban összenyomódnak, ha a nyomóerõ
növekszik. A levegõ is efféle test; s a jelen vizsgálat
elsõsorban a levegõre vonatkozik.
1.
Az elasztikus fluidumokhoz olyan szerkezetet rendelhetünk, amely összhangban
van összes ismert tulajdonságukkal, s így olyan tulajdonságaikat
is megvizsgálhatjuk, amelyeket még nem tanulmányoztunk
elegendõen. Az elasztikus fluidumok tulajdonságai a következõk:
1. nehezek; 2. minden irányban kiterjednek, ha szabadon mozoghatnak;
3. folyamatosan egyre jobban összenyomódnak, ha a nyomóerõ
növekszik. A levegõ is efféle test; s a jelen vizsgálat
elsõsorban a levegõre vonatkozik.
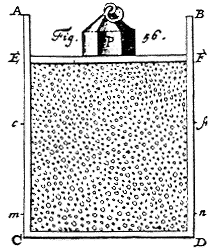 2. Tekintsük
a függõleges helyzetû ACBD hengeres edényt,
amelyben EF dugattyú mozog, és a dugattyúra
P
súly nehezedik. Az ECDF üreg tartalmazzon nagyon kis
részecskéket, amelyek nagyon gyorsan mozognak ide-oda. Ezek
a részecskék midõn az EF dugattyúval
ütköznek, és ismételt ütközéseik
révén fenntartják, elasztikus fluidumot képeznek,
amely magától kiterjed, ha a P súlyt eltávolítják
vagy csökkentik; sûrûbbé válik, ha a súlyt
növelik, és a gravitáció ugyanúgy vonzza
a vízszintes
CD fenéklap felé, mintha nem rendelkezne
elasztikussággal: tehát akár nyugalomban vannak, akár
keverednek a részecskék, nem veszítik el súlyukat,
ezért a fenéklap nemcsak a fluidum súlyát,
hanem elasztikusságát is megtartja. Ilyen fluidumnak tekintjük
most a levegõt, melynek tulajdonságai megegyeznek az elasztikus
fluidumok imént feltételezett tulajdonságaival, és
ezekkel a levegõ más ismert tulajdonságait is megmagyarázzuk,
s olyanokra is rámutatunk, amelyeket eddig nem vettek kellõképpen
figyelembe.
2. Tekintsük
a függõleges helyzetû ACBD hengeres edényt,
amelyben EF dugattyú mozog, és a dugattyúra
P
súly nehezedik. Az ECDF üreg tartalmazzon nagyon kis
részecskéket, amelyek nagyon gyorsan mozognak ide-oda. Ezek
a részecskék midõn az EF dugattyúval
ütköznek, és ismételt ütközéseik
révén fenntartják, elasztikus fluidumot képeznek,
amely magától kiterjed, ha a P súlyt eltávolítják
vagy csökkentik; sûrûbbé válik, ha a súlyt
növelik, és a gravitáció ugyanúgy vonzza
a vízszintes
CD fenéklap felé, mintha nem rendelkezne
elasztikussággal: tehát akár nyugalomban vannak, akár
keverednek a részecskék, nem veszítik el súlyukat,
ezért a fenéklap nemcsak a fluidum súlyát,
hanem elasztikusságát is megtartja. Ilyen fluidumnak tekintjük
most a levegõt, melynek tulajdonságai megegyeznek az elasztikus
fluidumok imént feltételezett tulajdonságaival, és
ezekkel a levegõ más ismert tulajdonságait is megmagyarázzuk,
s olyanokra is rámutatunk, amelyeket eddig nem vettek kellõképpen
figyelembe.
3. A henger alakú üregben lévõ részecskék
számát gyakorlatilag végtelennek tekintjük. Feltételezzük,
hogy az ECDF teret közönséges levegõ tölti
be, és minden mérésünkben ezt tekintjük
összehasonlítási alapnak: tehát az a P
súly, amely a dugattyút EF helyzetben tartja, nem
különbözik a hengerre nehezedõ levegõ nyomásától,
melyet a továbbiakban P-vel jelölünk.
Meg kell jegyeznünk, hogy ez a nyomás nem pontosan egyenlõ
az EF dugattyúra nehezedõ függõleges levegõoszlop
abszolút súlyával, amint sok szerzõ kellõ
körültekintés hiányában feltételezi.
A levegõoszlop súlya úgy aránylik a föld
felszínét körülvevõ légkör súlyához,
mint a dugattyú felülete a föld felszínéhez.
4. Tekintsük azt a p súlyt, amely
az ECDF-ben lévõ levegõt az eCDf térre
nyomja össze, és tegyük fel, hogy a részecskék
sebessége a levegõ mindkét állapotában,
a természetes és az összenyomott állapotban is
ugyanaz. Legyen EC=1 és eC=s. Ha az EF dugattyú
ef
helyzetbe mozdul el, a fluidum két ok miatt is nagyobb erõfeszítést
látszik kifejteni: elõször azért, mert a részecskék
száma most nagyobb az õket tartalmazó térhez
képest, másodszor azért, mert minden egyes részecske
gyakrabban ütközik. Az elsõ ok miatti növekmény
kiszámításához feltételezhetjük,
hogy a részecskék nyugalomban vannak. Az EF helyzetû
dugattyúval szomszédos részecskék számát
tekintsük n-nek, akkor a dugattyú ef helyzetében
n
: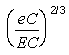 vagy n :
s2/3 lesz a számuk.
vagy n :
s2/3 lesz a számuk.
Meg kell jegyeznünk, hogy a fluidum sûrûsége
az alsó részben nem nagyobb, mint a felsõben, mert
a P súly végtelenül nagyobb a fluidum súlyánál:
ezért világos, hogy a fluidum ereje n és n:s2/3,
azaz s2/3 és 1 arányával adható
meg. A második ok miatti növekményt a részecskék
mozgása idézi elõ, és úgy tûnik,
hogy ütközéseik olyan mértékben gyakoribbak,
amilyen mértékben a részecskék közelebb
kerülnek egymáshoz: tehát az ütközések
száma fordítottan arányos a részecskék
felülete közötti átlagos távolsággal.
A következõkben ezeket az átlagos távolságokat
határozzuk meg.
Feltételezzük, hogy a részecskék gömbök.
A gömbök középpontjai közötti átlagos
távolságot D-vel jelöljük, ha a dugattyú
EF
helyzetben van, és d a gömb átmérõje.
Ekkor a gömbök felszíne közötti átlagos
távolság D–d. Nyilvánvaló azonban,
hogy ha a dugattyú az ef helyzetben van, a gömbök
középpontjai közötti átagos távolság 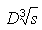 és
a gömbök felszíne közötti átlagos távolság
és
a gömbök felszíne közötti átlagos távolság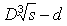 .
Tehát a második ok miatt az ECDF-beli természetes
levegõ ereje úgy aránylik az eCDf-beli öszenyomott
levegõ erejéhez, mint
.
Tehát a második ok miatt az ECDF-beli természetes
levegõ ereje úgy aránylik az eCDf-beli öszenyomott
levegõ erejéhez, mint 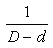 a
a 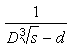 -hez, vagy
mint
-hez, vagy
mint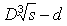 a D–d-hez.
Ha mindkét okot figyelembe vesszük, a jósolt erõk
úgy aránylanak egymáshoz, mint
a D–d-hez.
Ha mindkét okot figyelembe vesszük, a jósolt erõk
úgy aránylanak egymáshoz, mint 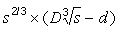 a
D–d-hez.
a
D–d-hez.
D és d arányára könnyen adhatunk
értéket, hiszen ha az EF dugattyút végtelen
súly nyomja le úgy, hogy a dugattyú abba az mn
helyzetbe
süllyed, ahol minden részecske érintkezik egymással,
és ha az mC vonalat m-mel jelöljük, azt
kapjuk, hogy D úgy aránylik d-hez, mint 1 a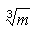 -hez. Ha ezt behelyettesítjük az elõzõ arányba,
azt találjuk, hogy az ECDF-beli természetes levegõ
ereje úgy aránylik az eCDf-beli összenyomott
levegõ erejéhez, mint
-hez. Ha ezt behelyettesítjük az elõzõ arányba,
azt találjuk, hogy az ECDF-beli természetes levegõ
ereje úgy aránylik az eCDf-beli összenyomott
levegõ erejéhez, mint 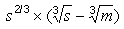 az
az 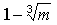 -hez, vagy
-hez, vagy 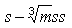 az
az 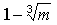 -hez.
Tehát
-hez.
Tehát 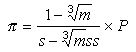 .
.
5. Az összes ismert ténybõl azt a következtetést
vonhatjuk le, hogy a természetes levegõ nagymértékben
összesûríthetõ és gyakorlatilag végtelen
kis térre nyomható össze; tehát feltehetjük,
hogy m=0, és innen p =P/s,
tehát a nyomást kiváltó súly fordítottan
aránylik a levegõ által elfoglalt térhez különbözõ
mértékû kompressziók esetén. Ezt a törvényt
számos kísérlet bizonyítja. Bizton elfogadható
arra a levegõre is, amely a természetes levegõnél
kevésbé sûrû. Hogy jelentõsen sûrûbb
levegõre is teljesül-e, nem vizsgáltam meg kellõképpen,
és megfelelõ pontosságú kísérletet
sem végeztek eddig erre nézvést. Igen nagy szükség
van az m értékét meghatározó
kísérletre, de ezt a kísérletet különleges
pontossággal és igen nagy nyomású levegõvel
kell elvégezni úgy, hogy a kompresszió során
a levegõ hõmérséklete állandó
maradjon.
6. A levegõ elasztikussága nemcsak a nyomás, hanem
a hõ hatására is nõ, s miután a hõ
a részecskék megnövekedett belsõ mozgásának
tekinthetõ, ha a változatlan térfogatú levegõ
elasztikussága növekszik, a levegõ részecskéi
élénkebb mozgásba kezdenek. Ez összhangban van
hipotézisünkkel, mert világos, hogy nagyobb P
súly szükséges a levegõ ECDF állapotban
való megtartásához, ha a részecskék
nagyobb sebességgel keverednek. Nem nehéz belátni,
hogy a P súlynak kétszer kell arányosnak lennie
a sebességgel, mert ha a sebesség nõ, nemcsak az ütközések
száma, hanem minden egyes ütközés erõssége
is egyaránt nõ, s mindkettõ arányos a P
súllyal.
Ezért ha a részecskék sebességét
v-vel
jelöljük, a dugattyút vvP súly tartja EF
helyzetben, és 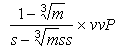 vagy
közelítõleg vvP/s tartja ef helyzetben,
mert amint láttuk, m nagyon kicsi az egyhez vagy az s
számhoz
képest.
vagy
közelítõleg vvP/s tartja ef helyzetben,
mert amint láttuk, m nagyon kicsi az egyhez vagy az s
számhoz
képest.
7. Ezt a szabályt, amelyet az elõzõ bekezdésben
ismertettem – ahol megmutattam, hogy a tetszõleges sûrûségû,
de adott hõmérsékletû levegõ elasztikussága
arányos a sûrûséggel, s a hõmérséklet
egyenlõ változásaival elõidézett elasztikusság-növekmények
arányosak a sûrûségekkel –, ezt a szabályt,
mondom, D. Amontons fedezte fel kísérleti
úton, és a Párizsi Tudományos Akadémia
Értekezéseiben közölte 1702-ben.
| Vissza |
http://www.kfki.hu/chemonet/
http://www.ch.bme.hu/chemonet/ |
 2. Tekintsük
a függõleges helyzetû ACBD hengeres edényt,
amelyben EF dugattyú mozog, és a dugattyúra
P
súly nehezedik. Az ECDF üreg tartalmazzon nagyon kis
részecskéket, amelyek nagyon gyorsan mozognak ide-oda. Ezek
a részecskék midõn az EF dugattyúval
ütköznek, és ismételt ütközéseik
révén fenntartják, elasztikus fluidumot képeznek,
amely magától kiterjed, ha a P súlyt eltávolítják
vagy csökkentik; sûrûbbé válik, ha a súlyt
növelik, és a gravitáció ugyanúgy vonzza
a vízszintes
CD fenéklap felé, mintha nem rendelkezne
elasztikussággal: tehát akár nyugalomban vannak, akár
keverednek a részecskék, nem veszítik el súlyukat,
ezért a fenéklap nemcsak a fluidum súlyát,
hanem elasztikusságát is megtartja. Ilyen fluidumnak tekintjük
most a levegõt, melynek tulajdonságai megegyeznek az elasztikus
fluidumok imént feltételezett tulajdonságaival, és
ezekkel a levegõ más ismert tulajdonságait is megmagyarázzuk,
s olyanokra is rámutatunk, amelyeket eddig nem vettek kellõképpen
figyelembe.
2. Tekintsük
a függõleges helyzetû ACBD hengeres edényt,
amelyben EF dugattyú mozog, és a dugattyúra
P
súly nehezedik. Az ECDF üreg tartalmazzon nagyon kis
részecskéket, amelyek nagyon gyorsan mozognak ide-oda. Ezek
a részecskék midõn az EF dugattyúval
ütköznek, és ismételt ütközéseik
révén fenntartják, elasztikus fluidumot képeznek,
amely magától kiterjed, ha a P súlyt eltávolítják
vagy csökkentik; sûrûbbé válik, ha a súlyt
növelik, és a gravitáció ugyanúgy vonzza
a vízszintes
CD fenéklap felé, mintha nem rendelkezne
elasztikussággal: tehát akár nyugalomban vannak, akár
keverednek a részecskék, nem veszítik el súlyukat,
ezért a fenéklap nemcsak a fluidum súlyát,
hanem elasztikusságát is megtartja. Ilyen fluidumnak tekintjük
most a levegõt, melynek tulajdonságai megegyeznek az elasztikus
fluidumok imént feltételezett tulajdonságaival, és
ezekkel a levegõ más ismert tulajdonságait is megmagyarázzuk,
s olyanokra is rámutatunk, amelyeket eddig nem vettek kellõképpen
figyelembe.
 1.
Az elasztikus fluidumokhoz olyan szerkezetet rendelhetünk, amely összhangban
van összes ismert tulajdonságukkal, s így olyan tulajdonságaikat
is megvizsgálhatjuk, amelyeket még nem tanulmányoztunk
elegendõen. Az elasztikus fluidumok tulajdonságai a következõk:
1. nehezek; 2. minden irányban kiterjednek, ha szabadon mozoghatnak;
3. folyamatosan egyre jobban összenyomódnak, ha a nyomóerõ
növekszik. A levegõ is efféle test; s a jelen vizsgálat
elsõsorban a levegõre vonatkozik.
1.
Az elasztikus fluidumokhoz olyan szerkezetet rendelhetünk, amely összhangban
van összes ismert tulajdonságukkal, s így olyan tulajdonságaikat
is megvizsgálhatjuk, amelyeket még nem tanulmányoztunk
elegendõen. Az elasztikus fluidumok tulajdonságai a következõk:
1. nehezek; 2. minden irányban kiterjednek, ha szabadon mozoghatnak;
3. folyamatosan egyre jobban összenyomódnak, ha a nyomóerõ
növekszik. A levegõ is efféle test; s a jelen vizsgálat
elsõsorban a levegõre vonatkozik.
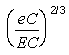 vagy n :
s2/3 lesz a számuk.
vagy n :
s2/3 lesz a számuk.
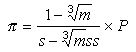 .
.
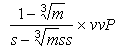 vagy
közelítõleg vvP/s tartja ef helyzetben,
mert amint láttuk, m nagyon kicsi az egyhez vagy az s
számhoz
képest.
vagy
közelítõleg vvP/s tartja ef helyzetben,
mert amint láttuk, m nagyon kicsi az egyhez vagy az s
számhoz
képest.