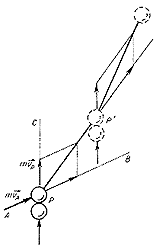
poligon alakú pályára kény-
szeríthetjük. Ennek határesete
a görbe vonalú pályán való
mozgás
Természet Világa, 127. évfolyam, 1. szám, 1996
SIMONYI KÁROLY
... az egek és tengerek minden jelensége
(HUYGENS, NEWTON)
Giordano Bruno máglyahalála, a Galilei-per, a kopernikuszi gondolat kiteljesedése, ezek a 17. század történései. Az események itt már felgyorsulnak. A század elején még megégetnek valakit a végtelen világ víziójáért, a század végén pedig mind a fizikai törvények rendszere, mind a matematikai eszköztár készen áll arra, hogy egy Holdra-szállás, vagy akár egy Mars-utazás pályaadatait meghatározhassuk. Ehhez azonban el kellett távolítani az ideológiai akadályokat, ki kellett alakítani a tudományos kutatás adekvát módszerét; az elmélet és kísérlet, a ráció és empíria helyes arányát és közben egymáshoz csatlakozva, egymással vitázva konkrét, kvantitatíve megfogalmazható eredményeket kellett felmutatni. A 17. század Iegtöbb tudósa még szaktudós és filozófus is volt, csak a század végén jelentek meg a szakfizikusok, mint amilyen Huygens vagy Newton, de kutatási módszerük, elveik a filozófiának is örökbecsû részei. A 17. századot a tudománytörténészek a zsenik századának szokták nevezni. Nevüket iskoláskönyveink is ôrzik: Kopernikusz, Kepler, Galilei, Bacon, Descartes, Pascal, Fermat, Huygens, Newton. Az ô hôsi erôfeszltéseikrôl, sikereikrôl és kudarcaikról szól az a négy elôadás, melyet a Természet Világa közread egymást követô hónapokban ...
A 17. század második felében a szaktudományok kutatóinak végleg nem kellett törôdniük semmiféle ideológiával, sem az arisztotelizmussal, sem a szerzôje szándéka szerint azt felváltani hivatott dékartizmussal. Ez utóbbit lassan-lassan éppen olyan pejoratív mellékzöngével kezdték emlegetni, mint korábban az arisztotelizmust. Pozitív hatása azonban észrevétlenül is érvényesült: felébresztette az emberekben az igényt a tiszta fogalmak, a tiszta fogalmakat használó világos okfejtés iránt: a clare et distincte követelmény szinte szlogenné vált. De descartes-i örökség a fizikában az igény a mechanikai világmagyarázat iránt. Ezt az irányzatot Newton késôbb még kihangsúlyozza: a világ jelenségei az anyagi testek között ható erôk és ezek hatására létrejövô mozgások összessége. Még a 19. század végén is olyan nagy tudós, mint Kelvin kijelentette, hogy csak akkor ért meg egy jelenséget, ha arról mechanikai modellt tud készíteni. Az elektromágneses térrôl nem tudok ilyen modellt készíteni, így nem is értem hangoztatta.
Az arisztotelizmus és a dékartizmus természetesen nem halt ki egészen; visszavonult az egyetemek falai közé, és ott elsôsorban a dékartizmus volt sokáig az uralkodó eszmerendszer. Így pl. egy 1676-ban kifejezetten az egyetemi ifjúság számára in usum juventutis academicae írt könyv ezzel a descartes-i mottóval indul: Semmit sem állítok, semmit sem akarok elhitetni senkivel, hacsak világosan és megcáfolhatatlanul az ész meg nem gyôzött annak igaz voltáról.
Tagadhatatlan, hogy a szerzô azon igyekezete, hogy a logikával kezdje a metafizikán, teológián át egészen az ütközési törvényekig, sôt a mágneses jelenségekig, minden ismeretet 1200 oldalon, egységes keretbe foglalva tárgyaljon, nagyon imponáló. Eltûnôdhetünk azonban azon, hogy a tudós professzor hogyan tudta összeegyeztetni a könyv mottójával azon állítását, amely a De Angelis et Daemonibus fejezetben található, hogy ti. az angyalok teljes létszáma, 9 értékes jegyre megadva, éppen 301 655 172 fô.
Amíg a középkorban az egyetemek a pezsgô tudományos élet központjai voltak, az eljövendô 23 évszázadra kiestek ebbôl a szerepbôl. Ezt a szerepet a tudományos társaságok, folyóiratok vették át. Itáliában már korábban mûködtek tudós társaságok: így többek között az 1603-ban Rómában megalakult Accademia dei Lincei, vagy a Firenzében 1657-ben alapított Accademia del Cimento. 1660-ban megalakult az angol Royal Society, 1666-ban az Academie des Sciences. 1665-ben megindult a Philosophical Transactions folyóirat, ugyanebben az évben a Journal des Savants és végül 1682-ben Leibniz folyóirata, az Acta Eruditorum. A tudományos élet nagyon hasonlított a maihoz: a tudósok cikkeket küldtek be a folyóiratokhoz, leveleztek egymással, feladatokat tûztek ki, prioritási harcokba bonyolódtak, intrikáltak, lobbiztak, legtöbbször nemzeti alapon.
A tudós társaságok rendszerint jól körülhatárolták tevékenységük körét, hogy elkerüljék az általuk terméketlennek tartott vitákat, mintegy felosztva ezzel a szellemi tevékenységeket az egyetemek és a tudós társaságok között. Hooke a szilárdságtan Hooke-törvényének megalkotója így határozza meg a Royal Society feladatát:
A Royal Society hivatása és célja, hogy elômozdítsa a természet dolgainak, valamint a kézmûvességnek, iparnak, mechanikai ügyességeknek, mérnöki munkának, úgyszintén a találmányoknak jobb megismerését kísérletek útján (nem keverve bele teológiát, metafizikát, erkölcsöt, politikát, grammatikát, retorikát vagy logikát). Továbbá: hogy megvizsgáljon a természetre, matematikára vagy mechanikára vonatkozó minden rendszert, elméletet, elvet, hipotézist amelyet bármely jelentôs szerzô, legyen az régi vagy modern, kitalált, feljegyzett vagy gyakorolt.
De a szintézis vágya nyíltan vagy titokban a szûk látókörû szaktudósban is él:
És mindezt abból a célból, hogy így össze lehessen állítani egy megbízható filozófia teljes rendszerét, amely meg tud magyarázni a természettel és a mesterségekkel kapcsolatos minden jelenséget és ésszerûen számot tud adni a dolgok okairól.
A 17. század harmadik negyedében a nemzetközi tudományos élet legismertebb és legelismertebb alakja a holland Huygens.
Tehetségérôl, mûveirôl, jelentôségérôl szuperlatívuszokban kellene beszélnünk, de vigyázni kell a jelzôkkel. Nem szabad elfelejtenünk, hogy a 17. század a géniuszok százada, amelyben valamilyen nézôpontból jó néhány tudóst megillet a legmagasabb értékítélet:
Kepler, a legcsapongóbb fantáziájú,
de legpontosabb és legfegyelmezettebb megfigyelô;
Galilei, a józan, határozott célkitûzésû,
azon belül a legmodernebb metódusú kutató;
Descartes, a saját elméletének foglya, de a
legátfogóbb, a legnagyobb hatású;
Pascal, akiben az elméleti, a kísérleti adottság
és az írói készség a legharmonikusabb;
és végül még hátravan a század
óriása, az összehasonlíthatatlan, a legnagyobb:
Newton.
Hol van köztük Huygens helye? Elôször is le kell szögeznünk, hogy Huygens nem filozófus, nem irodalmár, szaktudós: fizikus és matematikus, akárcsak Arkhimédész, akihez módszerét és szerepét hasonlítani szokták.
Huygensszel lett a fizika mai értelmben vett egyetemi szintû: megállapításai fényelméletének kvalitatív vonatkozásaitól eltekintve túlmennek a középiskolai anyagon és az egyetemen oktatott mechanika szerves részeivé váltak; és vele vált a fizika olyan szaktudománnyá, amelynek mûvelése és elôrevitele egy ember teljes energiáját leköti. A filozófiatörténetben talán az egy kortárs, Leibniz kivételével a fizikusok csak mellékalakok, és fordítva, a filozófiatörténet hôseinek kevés eredményét tudják a fizikusok felhasználni.
Nem általános filozófiai elvekbôl indul ki. Egyszerû, szemléletes, számszerûen is megfogalmazott fizikai elveket állít gondolatmenetei élére. Eredményei kivétel nélkül ma is helytállók, a gyakorlatba átvihetôk, és Huygens igen sokat át is vitt. Elôdeire, elsôsorban Galileire épített, és bármennyire is tiltakozott ellene igen nagy hatással volt rá Descartes. Kutatási irányukat egyenes vonalban vitte a betetôzés, a newtoni mechanika felé. Ahol vizsgálatai nem torkollottak közvetlenül ide, mint amilyen a kinetikus és .potenciális energia egymásba alakulásának felismerése, ott a newtoni mechanikából késôbb levezetett eredményeket anticipálta.
Most már megadhatjuk Huygensnek is a jelzôk szuperlatívuszát: a század legfegyelmezettebb, legkritikusabb szellemû és legtöbb konkrét eredményt felmutató fizikusa az egyetlen Newtont kivéve.
Hogy mennyire modern filozófiai beállitottságú volt, azt a Traité de la Lumière, vagyis Értekezés a fényrôl címû munkájának elôszava bizonyítja. Ez az elôszó helyet kaphatna bármely mai fizikakönyvben. A humán értelmiségiek számára ennél világosabban nem lehet megforgalmazni a fizika módszerét. Ez a módszer elkerüli a baconi "gyûjtögessük a tényeket" és a descartes-i "elefántcsonttoronyba zárkózva gondolkodjunk" tanácsok buktatóit. Egyben rámutat arra, hogy a fizikus a közhiedelemmel ellentétben egyáltalán nem tartja megállapításait abszolút igaznak, csak valószínûnek. Hogy ez a valószínûséggel kifejezett bizonytalanság mit jelent a gyakorlatban, azt egy Holdraszállásvisszatérés manôver realizálása szemléltetheti. Íme az elôszó:
Amíg a geométerek állításaikat biztos és megtámadhatatlan elvekbôl vezetik le, addig itt az elveket azok a következtetések bizonyítják, amelyeket belôlük le lehet vonni; ezen dolgok természete nem engedi; hogy másképp lehessen csinálni. Ilyen módon mindig el lehet érni a valószínûség olyan fokát, amely gyakran alig kevesebb, mint a teljes bizonyítás. Ez a helyzet például akkor, ha a dolgok, amelyeket levezettünk a feltételezett elvek segítségével, tökéletesen megfelelnek azon jelenségeknek, melyeket a megfigyelés szemünk elé tárt; különösen, ha ezek igen nagy számúak, továbbá és fôleg, ha el tudunk képzelni és meg tudunk jósolni olyan új jelenségeket, amelyeknek az alkalmazott hipotézisekbôl kell következniök és ha úgy találjuk, hogy a tények megfelelnek jóslásunknak.
Azok a tudósok, akikrôl eddig már beszéltünk, minden bizonnyal nagyon megsértôdnének azon, hogy jelentôségüket azzal mérjük, hogy mennyire készítették elô a Newtonhoz vezetô utat, tehát hogy mennyire voltak Keresztelô Jánosai a századvég Messiásának, Newtonnak. Vonatkozik ez különösen Descartes-ra, pedig az ô ütközési törvényei még a maguk hibás voltukban is jelentôséget éppen azzal nyertek, hogy elôkészítették ezt az utat:
Galilei kinematikai megállapításait ma is úgy tanuljuk tanítjuk, ahogy nála szerepelnek. Azok nem voltak hibásak. Miért nem lehetett közvetlenül csatlakozni hozzájuk?! Ha elôrehozzuk a végeredményt, Newton mozgástörvényét, amely szerint nagy erô nagy gyorsulást hoz létre, akkor felmerül a kérdés, hogy a nagyobb súly, amely kétségkívül nagyobb erôt jelent, miért nem okoz nagyobb gyorsulást? Miért esik minden test egyforma gyorsulással és így természetesen egyforma végsebességgel. Ennek a ténynek leszögezése Galilei idejében forradalmi gondolat volt, mert hozzájárult az arisztotelizmus megdöntéséhez, viszont nem mutatta meg a kibontakozáshoz vezetô utat. Galilei kortársai közül már többen észrevették, hogy itt a tömegnek kettôs szerepe van: egyrészt valami aktív, ható erô jellegû és valami passzív, ami ennek az erônek ellenszegül. Ma az aktív szereplôrôl azt mondjuk, az a gravitáló tömeg, a passzívról pedig, hogy a tehetetlen tömeg. Közvetlen szemléletünk számára a különbség így mutatható meg. Ha egy súlyos golyót kezünkben tartunk, akkor az erô, amit ilyenkor izmainkban érzünk, a súlyos tömeggel arányos. Ha a golyót egy vízszintes síklapra helyezzük, akkor kiküszöböltük a gravitációs vonzás hatását. Ha most a golyónak sebességet akarunk adni és gyorsítjuk, amit ilyenkor érzünk izmainkban, az a tehetetlen tömeggel arányos. Még szemléletesebb, de itt ismereteinkbôl még többet kell elôrehoznunk, a következô kísérlet. Forgó zsámolyon ülünk, mindkét kezünkben súlyzót tartunk. Ezek gravitáló tömege húzza kezünket függôlegesen lefelé, ha a zsámoly áll. Meghatározott forgássebesség mellett a golyók távolabb kerülnek a forgáscentrumtól; kissé felemelkednek úgy, hogy karunk meghatározott szöget zár be a forgástengellyel. A karunkat kifelé húzó erô a tehetetlen tömeggel arányos. Sietve megjegyezzük, hogy Newton ilyen jellegû kísérlettel mutatta ki a tehetetlen tömeg és a gravitáló tömeg azonos voltát: adott forgássebesség mellett a kitérés szöge, függetlenül a felfüggesztett testek minôségétôl, súlyától, azonosnak adódik, és ebbôl a két tömeg azonossága következik. Még messzebb, egészen a huszadik századig elôrenyúlva: ezt az azonosságot legpontosabban Eötvös Loránd mérte meg és ez az azonosság szolgál az általános relativitás alapgondolatául.
A ma mindennapjainak látványos tudományos vonzatú eseményeinél, az ûrhajózásnál a súlytalanság állapotában fellépô jelenségek megértéséhez is a tömeg ezen kétféle aspektusának tisztázása vezet.
De visszatérve a 17. század közepe tájára: A Galilei által tárgyalt mozgások kinematikájából a tömeg bújtatott kéttôs szerepe miatt nem lehetett a dinamikát kifejleszteni.
 |
| Ütközések sorazatával a testet poligon alakú pályára kény- szeríthetjük. Ennek határesete a görbe vonalú pályán való mozgás |
Az ütközésnél viszont csak a tehetetlen tömeg játszik szerepet. Ugyanakkor a mozgásállapotot leíró fogalmak közül mint amilyenek a pálya, a sebesség, a sebességváltozás, vagyis gyorsulás a már mintegy ôsidôk óta kikristályosodott fogalmak, mint az egyenes vonalú pálya és az állandó sebesség szerepelnek. Így a sebesség változása is, amely egy ütközésnél a fellépô rugalmas erôk hatására létrejön, kvantitatív jelentést kap. Még Newton is a mozgástörvény felállításához vezetô elsô meggondolásaiban a görbe vonalú pályán való mozgást is rövid idôközökben egymás után következô ütközések eredôjeképpen fogta fel.
De térjünk vissza Huygenshez. Elôször is szisztematikusan tárgyalta Galileinek a lejtôn való, ill. a szabadeséssel kapcsolatos vizsgálatait, általánosította néhány megállapítását tetszés szerinti vezérgörbéjû (tehát nem sík) lejtôre, megállapította az ütközés máig érvényes szabályait, néhány zseniálisan választott kiinduló elv segítségével. Ezekrôl a kiinduló elvekrôl van szó könyve idézett elôszavában. Éspedig:
Egy test mindaddig megmarad az egyenes vonalú egyenletes mozgás állapotában, míg egy külsô erô nem kényszeríti ezen mozgásállapot megváltoztatására. Ez a tehetetlenségi vagy inerciatörvény. Galilei sejtette, Descartes tudta, Huygens, majd Newton axióma rangjára emelte.
A mozgások, ha nincs súrlódás, megfordíthatók. Ha egy test nyugalmi állapotból elindul és egy lejtô aljára érkezve az ottani sebességével visszafordítjuk, ugyanolyan magasra fog érkezni:
Ha a testek rendszere kizárólag súlyuk hatására mozgásba jön, súlypontjuk sohasem kerülhet magasabbra, mint amilyen kezdô állapotban volt.
Végül talán a legmélyebb tartalmú megállapítás: a mechanikai jelenségek mint amilyen pl. az ütközés jelensége ugyanúgy folynak le két egymáshoz képest egyenletes sebességgel mozgó koordináta-rendszerben. A koordináta-rendszerek ekvivalenciájának ilyen határozott kimondásával Huygensnél találkozunk elôször. Ezt az ekvivalenciát a 20. század elsô éveiben a relativitáselmélet kérdôjelezi meg, ill. pontosítja.
Huygens egyik legszebb eredménye: A fenti alapfeltevések segítségével felír egy összefüggést, amelynek egyes tagjait ma mint az egyes testek kinetikus energiáját, más tagokat mint a potenciális energiát értelmezzük, az egész összefüggésben pedig mint a kinetikus és potenciális energia összegének állandóságát, tehát végül is az energiamegmaradás tételét ismerjük fel. Hangsúlyozzuk, hogy ilyen értelmezést mi, az utókor adunk az egyenletnek, Huygens csak levezette. Ezek az eredmények nem vezettek közvetlenül a newtoni törvények felállításához: megkerülték azt és szinte elébevágtak.
Huygens Galileinek az inga mozgására vonatkozó megállapításait is korrigálta a fenti elvek segítségével: Galilei még azt hitte, hogy az inga lengésideje az inga kitérésétôl függetlenül állandó; holott ez a megállapítás csak kis kitérésekre igaz. Huygens egyrészt megadta a lengésidô pontos, ma a középiskolás törzsanyag részeként szereplô képletét, de megkonstruálta azt az ingát, amelynek lengésideje független a kitéréstôl: ez a cikloidális inga. Ezt és a fizikai inga elméletét csak megemlítjük, mert ezek már egyetemi szintû tárgyalást igényelnek.
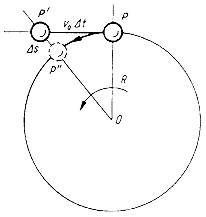 |
| Az egyenletes körmozgás gyorsulását Huygens így vezette le: a Ds = (1/2) (vo2/R) Dt2 közelítô összefüggést a szabadesés s = (1/2) gt2 képletével hasonlította össze; így adódik ki az a = vo2/R kapcsolat |
Közvetlenül a Newton felé vezetô út mentén feküdt Huygensnek a körmozgással kapcsolatos eredménye. Huygens megállapította egy körpályán egyenletes sebességgel mozgó test gyorsulását. Minden bizonnyal furcsán hat, hogy egy állandó sebességgel mozgó test gyorsulásáról beszélünk. De éppen a legegyszerûbb görbe vonalú pályán, a körpályán mozgó test esetében érhetô leginkább tetten az a tény, hogy a sebesség irányított (vektor) mennyiség, sebességváltozás, tehát gyorsulás akkor is fellép, ha csak az iránya változik. Nemcsak az eredményt, de a levezetést is Huygens módszere szerint találjuk igen sok középiskolás tankönyvben. Huygens úgy tekintette, hogy ha a kötél nem húzná a középpont felé a testet, az érintôlegesen elrepülne. A valóságban elsô közelítésben parabolapályát ír le (a kört az érintési pont helyén parabolával helyettesítjük). Ezt most már össze lehet hasonlítani a ferde hajítás parabolájával, és így a gyorsulás meghatározható. A képletet Newton is levezette és sajnálattal állapította meg, hogy Huygens megelôzte.
Huygens eddig felsorolt eredményei érvényességüket nem; de aktualitásukat, fontosságukat elvesztették. A fénytannal kapcsolatos megállapításai ezzel szemben ma is aktuálisak, a Huygens-elv még az antennarendszerek elméletébe, általában az elektromágneses sugárzás elméletébe is belekerült. Huygens fogalmazta meg élesen és adott mindmáig elfogadható választ arra a kérdésre, hogy 1. hogyan terjed a fény; 2. mekkora a terjedési sebessége. Ezzel megindul egy hosszú és termékeny vita a fény kettôs természetérôl: vajon a fény korpuszkulák, részecskék kibocsátásából és tovahaladásából, vagy pedig egy rezgési állapot tovaterjedésébôl áll? A hullámrészecske dualizmus vita megindulása tehát Huygenstôl származtatható. Huygens nagyon határozottan kiáll mai nómenklatúránkkal kifejezve a hullámfelfogás mellett: a fény terjedése úgy jön létre, hogy a fényforrás mintegy ismételten meglöki a körülötte lévô megint a mai nómenklatúránkkal élve éter részecskéit, azokat "gerjeszti", azok ezeket a lökéseket továbbadják, tehát a fény egy mozgásállapot terjedése, a fényt hordozó anyag részecskéi azonban helyben maradnak. Huygens számára a legfôbb megmagyarázandó kérdés az volt, amit eddig triviálisnak tartottak: miként lehetséges a fény egyenes vonalú terjedése? Talán sokan emlékeznek még azokra a középiskolás tankönyvekben szereplô ábrákra, ahol a kialakult hullámfelület mindegyik pontja egy-egy gerjesztô centrumnak tekinthetô, és az így kialakult hullámfelületek burkoló felülete lesz az új hullámfelület. Meggyôzô, szemléletes ábrákat lehet rajzolni arról, hogy a fény a sûrûbb közegben lassabban kell hogy terjedjen, ha azt akarjuk, hogy a fénysugár a beesési normális felé törjön.
Huygens könyvében szerepel Olaf Romer gondolatának leírása, amellyel a Jupiter-holdak keringési idejének szabályszerû változásából meghatározta a fény terjedési sebességét.
| A fizika kultúrtörténetébôl Kémiatörténet |
http://www.kfki.hu/chemonet/ http://www.ch.bme.hu/chemonet/ |