
dans le vide) kísérlete.
Pascal a Torricelli-féle
elrendezést egy vastagabb
csô Torricelli-ûrjében he-
lyezte el, és ezzel ezen
belsô berendezés számára
változó külsô nyomást
tudott létrehozni Ievegô
bebugyborékoltatásával
Természet Világa, 126. évfolyam, 12. szám, 1995
SIMONYI KÁROLY
Az én módszerem jobb, mint a
szokásos
(DESCARTES, PASCAL)
1650 körül még egy – ideológiai vonzattal bíró – jelenség megmagyarázása hátra volt: ez a vákuum problémája. Az üres tér fogalmilag és így fizikailag is lehetetlen, hirdeti az arisztotelizmus. A vákuumtól való irtózás, a horror vacui adott magyarázatot a szivattyúk mûködésére. Az ezzel foglalkozó szakemberek azonban észrevették, hogy a szivattyúik csak bizonyos mélységig tudnak dolgozni. Valami úgy látszik határt szab a horrornak, az irtózásnak. Víz esetén ez a magasság 10 m körül van. Az utat a helyes megoldáshoz Torricelli 1643-ban végzett kísérlete mutatta meg: Ha a higannyal telt, egyik végén zárt, a másik végén nyitott üvegcsövet nyitott végével lefelé egy higannyal töltött tálba merítjük, akkor azt találjuk, hogy a higanyszál elválik a felsô lezáró felülettôl, és 76 cm magasságban megáll. A higannyal végzett kísérletnek azért van olyan jelentôsége, mert a 10 m magas vízoszloppal szemben ez a rövid higanymagasság sokkal könnyebben elvégezhetô kísérleteket tesz lehetôvé.
A másik jelentôsége a higanynak az az elsô pillanatban jelentéktelennek látszó tény, hogy éppen a kis méretek miatt a csô üvegbôl készíthetô, és így látni lehet, hogy mi történik az üvegcsô belsejében. A vízszivattyú szivócsövében ugyanis még azt sem lehetett megállapítani, hogy a víz hozzátapad-e a dugattyúhoz, vagy ott valóban valamilyen ûr keletkezik. A következô évtized legizgalmasabb kérdése, amely a legszenvedélyesebb viták tárgya lett, éppen a Torricelli-ûr volt, tehát a higany felszíne és az üveg felsô fala közötti térrész. A kérdés egyrészt az volt, hogy mi van az ûrben, másrészt az, hogy miért áll meg a higany egy egészen meghatározott magasságban. Az elôzôre elvileg azt a két választ lehetett adni: ott vákuum van, illetôleg ott nincs vákuum, hanem valamilyen anyagféleség. Az utóbbira pedig: a jelenség okát a levegô nyomásában kell keresni, illetôleg a horror vacuiban. Ezeket a lehetséges válaszokat még össze is lehet kombinálni: valóban mindegyik lehetséges kombinációnak voltak neves képviselôi. Az Arisztotelész-hívôk természetesen azt válaszolták, hogy vákuum nem lehetséges, tehát a Torricelli-féle ûrben jelen kell lennie az anyag valamilyen fajtájának. A jelenség okát pedig a most már mérhetô kvalitássá szelídített horror vacuiban kell keresni. Descartes maga és követôi a jelenség okát – helyesen – a külsô légnyomásban látták, viszont azt állították, hogy a Torricelli-féle ûrben sem lehet vákuum; végül Pascalban lassan és igen gondos, sokrétû kísérletezés után alakult ki a helyes meggyôzôdés: a jelenség oka a külsô levegô nyomása, és a Torricelli-ûrben vákuum van.
 |
| Pascal "ûr az ûrben" (vide dans le vide) kísérlete. Pascal a Torricelli-féle elrendezést egy vastagabb csô Torricelli-ûrjében he- lyezte el, és ezzel ezen belsô berendezés számára változó külsô nyomást tudott létrehozni Ievegô bebugyborékoltatásával |
A döntô kísérletet Pascal 1647-ben tervezte meg és az ô útmutatása alapján sógora végezte el a Puy-de Dome hegycsúcson. Pascal igen helyesen úgy okoskodott, hogy ha a higanyszál magasságát a levegô súlyából eredô légnyomás hozza létre, akkor a tengerszint feletti magasságtól függôen a higanyszál magasságának is csökkennie kell. A nagyon gondosan elvégzett kísérletek valóban azt mutatták, hogy a hegy lábánál hagyott mûszer és a 800 méterrel magasabban felállított mûszer higanyoszlopánál jól mérhetô, kb. 8 cm magasságkülönbség lép fel. Ez az 1648. szeptember 19-én elvégzett kísérlet a fizika "nagy" kísérletei közé tartozik. Pascal végül így vonja le a végsô konklúziót:
Arisztotelész tanítványai most összehordanak minden érvet, amely Mesterük, vagy a kommentátorok írásaiban található, hogy ezeket a dolgokat a horror vacuival magyarázzák, ahelyett hogy belátnák, hogy a tapasztalás az igazi mester, akit a fizikában követni kell, és hogy ez a kísérlet, amelyet a hegyekben végeztünk, felborította azt az általános hitet, hogy a természet irtózik a vákuumtól, és nyilvánvalóvá tette azt az ismeretet, amely most már soha nem vész el, hogy a természet egyáltaIán nem irtózik a vákuumtól, nem tesz semmit, hogy azt elkerülje, és hogy a Ievegô tömegének súlya az igazi oka mindazon dolgoknak, amelyeket eddig ezen képzelt oknak tulajdonítottak.
Az optika ideológiailag irreleváns tudomány. A töréstörvény sem különlegesen érdekes, mégis foglalkozunk vele, mert vele kapcsolatban bukkant fel elôször a fizikában egy új, nagy horderejû elv, amely a modern fizikának is nagy segítôje: a minimál-elvre vagy általánosságban az extremális-elvre gondolunk.
A töréstörvény: Ha a fénysugár egy ritkább közegbôl egy sûrûbb közegbe lép át, a határoló felületen megtörik és a beesési normálistól mért szögek szinuszainak aránya egy, a két közegre jellemzô állandó. Descartes a törvény levezetésénél feltéteIezte, hogy a sûrûbb közegben a fény gyorsabban terjed.
Ezt a feltételezést Fermat élesen bírálta: nyilvánvaló, hogy a sûrûbb anyag nagyobb ellenállást fejt ki a fény mozgásával szemben, és ezért benne a fény sebességének kisebbnek kell lenni. Ugyanakkor kiindulva abból a megfontolásból, hogy a természet igyekszik mindent a legegyszerûbb módon megvalósítani, megfogalmazta híres elvét, a Fermat-elvet:
A fénysugár két pont között azt a pályát választja, amelynek befutásához a legrövidebb idôre van szüksége. Azt, hogy egy ilyen elvbôl miként adódik ki a töréstörvény, az alábbi hasonlattat kíséreljük meg a szemlélethez közelebb hozni. Kirándulás alkalmával egy rét közepén állunk. Szemben velünk a réttôl egy hosszú egyenes barázdával elválasztott szántóföld, balra elôre, a barázdától messze, benn a szántáson egy csôszkunyhó áll. Vihar közeledik, igyekszünk a csôszkunyhóba a lehetô legrövidebb idô alatt eljutni. Torony iránt, javasolja valaki, az a legrövidebb út. Igen, de akkor viszonylag sokat kell mennünk a szántáson és ott lassabban haladunk. Akkor menjünk a réten (a nagyobb sebességünkkel) egészen addig a pontig, ahonnan merôlegesen a barázdára, a legrövidebb az út a csôszkunyhóig. Így viszont a megteendô össz út lesz túl hosszú. Ha teljesen ösztönösen cselekszünk, akkor is megtaláljuk többé-kevésbé helyesen a barázdán azt a pontot, ameddig a réten futunk, majd irányt változtatva eljutunk a kunyhóig. Ebben az egyszerû esetben nagyon könnyû utánaszámolni, hogy a Iegrövidebb idô alatt megtehetô út az Iesz, amelynél a barázdához érkezés szögének szinusza úgy aránylik a szántáson tovahaladás szinuszához, mint a réten való haladás sebessége a szántáson való haladás sebességéhez. A szögeket természetesen a barázdára emelt merôlegestôl kell mérni.
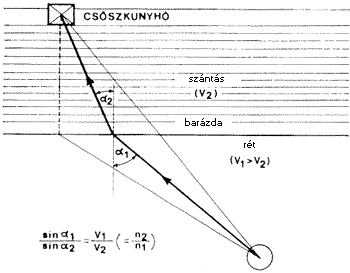
"Gondolatkísérlet" a Fermat-elv és a töréstörvény szemléltetésére
A fénysugár útjának meghatározásához a Fermat-elv akkor is alkalmazható, ha az anyag törésmutatója folytonosan változik.
Ennek a korszaknak kétségkívül Descartes volt legnagyobb alakja. Filozófiáját epigonok szajkózták és zsenik támadták. Búcsúzóul hallgassuk meg Voltaire értékelését.
[Egyes angol tudósok] azzal mertek elôhozakodni, hogy Descartes nem volt nagy geométer. Akik így beszélnek, szülôanyjukat bántalmazzák: Descartes éppen olyan nagy utat tett meg abból a pontból kiindulva, ahol a geometriát találta, addig a pontig, ameddig azt továbbvitte, mint amekkorát Newton tett meg utána: ô volt az elsô, aki felállította a görbék algebrai egyenletét. Geometriája ennek köszünhetôen ma már általánosan elterjedt, de a maga idejében olyan mély volt, hogy egyetlen professzor sem vállalkozott megmagyarázására és más nem is akadt, mint Schooten Hollandiában és Fermat Franciaországban, aki megértette.:. Nem tagadom, hogy Descartes úr többi mûvében nyüzsögnek a hibák... Filozófiája nem más, mint elmés regény, többé-kevésbé elfogadható a tudatlanok számára. Tévedett a lélek természetében, Isten létének bizonyításában, az anyag felfogásában, a mozgás törvényeiben, a fény termtészetében; hitt a velünk született ideákban, új elemeket talált ki, egy világot teremtett.
Nem túlzás, ha azt mondjuk, hogy még eltévelyedéseiben is tiszteletreméltó. Tévedett, de azt legalább módszeresen tette és következetes szellemben; lerombolta azokat az abszurd agyrémeket, amelyekkel kétezer év óta bolondították az ifjúságot; kora embereit megtanította gondolkodni, felhasználni saját maga ellen fegyevereit. Ha nem is fizetett jó pénzzel, már az is elég, hogy leleplezte a hamisat.
| A fizika kultúrtörténetébôl Kémiatörténet |
http://www.kfki.hu/chemonet/ http://www.ch.bme.hu/chemonet/ |