 |
 |
| 1. ábra | 2. ábra |
TUDOMÁNY ÉS VALÓSÁG
Ebben az esszében szeretném ismét ráirányítani a figyelmet egy olyan felfogásra, melyet – miután két évezreden át vezetôül szolgált természetértésünk számára –, diszkreditált a tudomány modern értelmezése. A valóság koncepciójáról beszélek. Manapság ritkán hallani azt, hogy a tudomány célja a természeti tények mögött rejlô valóság felfedezése. A tudomány modern eszménye az, hogy pontos matematikai összefüggést teremtsen az adatok között, figyelmen kívül hagyva, hogy ezen összefüggések tudományos érdekességét az adja, hogy a valóság valamilyen tulajdonságát teszik megfoghatóvá számunkra. Célom az, hogy felelevenítsem és a tudományos vizsgálódás elméletének középpontjába állítsam a valóság fogalmát.
Ez a feltámasztott valóságfogalom bevallottan különbözni fog letûnt elôdjétôl. Nem a minden látszat mögött rejtezô, jól kivehetô, szilárd alap többé, hanem olyasmi, amit csupán nagyjából ismerhetünk meg, s amihez meghatározhatatlan várakozások végtelen sora fûzôdik.
Mindenki tudja, hogy az ôsi elképzelést, mely szerint a Nap és a bolygók a Föld körül keringenek, Kopernikusz döntötte meg, és ô alkotta meg azt a rendszert, melyben a Nap áll a középpontban, s a bolygók, köztük a Föld, körülötte keringenek. Arról azonban nem esik szó, hogy Kopernikusz és követôi felfedezésének értelmezésével megteremtették a modern tudomány metafizikai alapjait. Nem esik szó róla, mert manapság a tudomány ezen alapjait többnyire megkérdôjelezik.
Jól emlékszünk a Kopernikusz és ellenfelei közti konfliktusra, mely Galileinek a Szent Offícium általi perbe fogásához vezetett. Tisztában kell lennünk azzal is, hogy a vita középpontjában a heliocentikus rendszer valóságosságának kérdése állt. Kopernikusz és követôi azt állították, hogy rendszerük valóságos képet ad a Napról és a körötte keringô bolygókról; ellenfeleik viszont azt mondták, hogy rendszerük nem több új számítási segédeszköznél.
Kopernikusz harminc éven át vonakodott közzétenni elméletét, fôként azért, mert tudta: ha elkötelezi magát a heliocentrikus rendszer valóságossága mellett, ezzel szembeszegült volna Arisztotelész tanításaival. 1543-ban, két évvel a mû megjelenése elôtt, egy Osiander nevû protestáns hitszónok levélben fejtette ki véleményét Kopernikusz rendszerének elôzetes ismertetéseire reagálva, s arra kérte Kopernikuszt, jelentse ki kereken, hogy a tudomány csupán a jelenségek leképezésére szolgáló hipotézisek megalkotására képes, a valóság megjelenítésére nem. Osiandernek késôbb sikerült egy elôszót csatolnia Kopernikusz kinyomtatott mûvéhez, melyben ismételten tagadta a kopernikuszi rendszer valóságosságát. A kérdés ugyanez maradt akkor is, amikor több mint fél évszázaddal késôbb Kepler védelmébe vette Tycho Brahét az ôt támadó Ursusszal szemben, és akkor is, amikor Galilei találta szemben magát Bellarmine bíborossal, majd VIII. Orbán pápával.
A kérdést, legalábbis világi részrôl, a kopernikuszi rendszer Newton-féle igazolása döntötte el. Ekkor bizonyosodott be, hogy Kopernikusznak és követôinek igaza volt. A rákövetkezô két évszázad modern mûvelt nagyközönsége a legnagyobb tisztelettel adózott a tudomány melletti rendíthetetlen kiállásuknak.
Még engem is ebben a szellemben neveltek, de akkoriban néhány érdemes szerzô már megkezdte aknamunkáját. A tudomány pozitivista kritikája, melyet Ernst Mach[1] kezdeményezett, Henri Poincaré[2] pedig lelkesen támogatott, azt hangoztatta, hogy amit Kopernikusz, Kepler és Galilei oly elszántan védelmeztek, illúzió volt. A radikális pozitivizmus tanítása szerint a tudomány pusztán funkcionális összefüggéseket teremt az általunk megfigyelt érzet-adatok között, és minden állítás, mely túlmegy ezen, bizonyíthatatlan. A megfigyelt tények közötti matematikai összefüggések alapját képezô valóság minden kézzelfogható tartalmat nélkülözô metafizikai elképzelés.
Az elmúlt fél évszázadban ezek a pozitivista megfontolások elôször a logikai pozitivizmusban nyertek kifejezést, mely szigorú kritériumokat kívánt teremteni minden empirikus állítás jelentésének és értékének megállapításához. De a logikai pozitivizmus ázsiója, negyvenes évekbeli fénykorát követôen, csökkenni kezdett, mivel célkitûzései kivihetetlennek bizonyultak. Elméleteit ezután egy sor módosítással felpuhították, vagyis lemondtak a tudományos állítások jelentését és értékét meghatározó formális kritérium keresésérôl. Az analitikus filozófia térhódítása teljessé tette ezt a lemondást azzal, hogy nem foglalkozott a tudomány kritikájával. Ekképpen a természettudomány lényegérôl és igazolásáról ma nincs semmiféle bevett elméletünk.
A pozitivista irányzattal számos szerzô szállt élesen szembe, köztük Max Planck[3] és Einstein[4], valamint Alexandre Koyré[5], a nagy tudománytörténész, ám ezen szerzôk kijelentései nem teremtették meg a tudomány valódi metafizikai alapját. Ez tehát az a szituáció, amelyben szemügyre veszem azt a kopernikuszi állítást, miszerint a heliocentrikus rendszer hû képet ad a valóságról. Rá fogok mutatni arra, hogy a valóság ezen felfogásában találhatjuk meg azt a valódi alapot, melyre a tudomány azóta épül, hogy Kopernikusz erre alapozva megteremtette a modern tudományt.
Hogy megmagyarázzam, miért gondolhatta Kopernikusz az általa javasolt új rendszert valóságosnak, kitérek a régi rendszer egyik fontos vonására, és arra, hogy az új rendszer miképpen viszonyult ehhez.
Ha egy bolygót estérôl estére megfigyelünk,
azt tapasztaljuk, hogy változtatja helyzetét az álló
csillagokkal benépesített égbolton. Ha az északi
féltekérôl nézzük, nagyjából
nyugatról kelet felé mozog, de mozgása nem egyenletes.
Hol gyorsabb, hol lassabb, olykor úgy tûnik, mintha visszafelé
mozogna, aztán folytatja útját keletre. Ilyesféle
hurkokat szabályos idôközönként ír
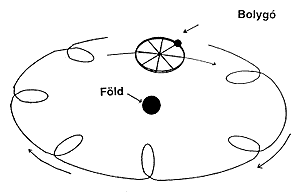
le. A ptolemaioszi rendszer ezt azzal magyarázta, hogy a bolygó
– ahelyett, hogy egyszerû körmozgást végezne –
úgy mozog ezen a körpályán, mint egy keréken
elhelyezkedô pont. Miközben a kerék megkerüli a
bolygót, saját tengelye körül is elfordul, és
így a Földrôl nézve úgy tûnik, mintha
hurkokat rajzolna bolygó körüli pályáján.
Ezeket a kerekeket epiciklusoknak nevezték, és itt leírt
típusuk talán a legfontosabb. (1. ábra) Az epiciklus
mozgásának útját deferensnek nevezik.
 |
 |
| 1. ábra | 2. ábra |
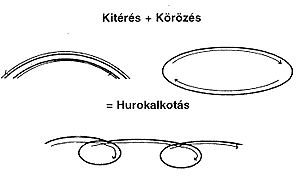
Az epiciklikus mozgás hatását úgy lehet
közelebbrôl elemezni, ha feltesszük, hogy a bolygó
egy idôre megszakította körpályáján
végzett keleti irányú mozgását. A földi,
mozdulatlan megfigyelô azt látja, hogy a bolygó az
epicikluson való elmozdulásának sebességtól
függôen kitér pályáján (2. ábra).
Ha ehhez a kitéréshez hozzáadjuk kelet-nyugati mozgását,
máris megkapjuk azokat a hurkokat, amelyeket a Földrôl
megfigyeltünk (3. ábra).
 |
 |
| 3. ábra | 4. ábra |
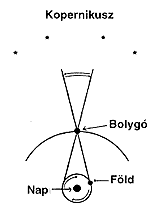
Kopernikusz alapötlete az volt, hogy ugyanezt a hatást kapjuk akkor is, ha feltesszük, hogy nem a bolygók mozdulnak el az epiciklus kerekei mentén, hanem a Föld forog a Nap körül. Ha megint csak magunk elé képzelünk egy bolygót keringés közben, majd a csillagos égbolton követjük képét, ez a kép ugyanolyan kitérést fog mutatni, mint amit a ptolemaioszi rendszer bolygóinál láttunk (4. ábra). Ha pedig ehhez a kitéréshez ismét hozzávesszük a bolygó keleti irányú keringését, a már megfigyelt hurkok rajzolódnak ki elôttünk. Ezek a hurkok azonban ezúttal csupán látszólagosak, nincs mögöttük semmiféle epiciklikus mozgás.
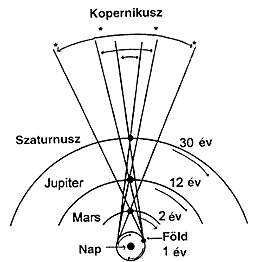
Hadd egészítsem ki a fentieket a ptolemaioszi rendszer néhány vonásával, melyeket Kopernikusz ismert. Elôször is, mindegyik fô epiciklust reprezentáló kerék ugyanazzal a sebességgel mozog körbe, és úgy találták, hogy az epiciklusok ezen egységes keringési ideje egy év. Tehát például egy olyan bolygó, mint a Mars, melynek keringési ideje megközelítôleg két év, egy hurkot tesz keringés közben, míg a Jupiter, melynek keringési ideje tizenkét év, tizenegy hurkot ír le, a Szaturnusz pedig, a maga harminc évig tartó körülfordulása
alatt huszonkilenc hurkot rajzol pályáján[6]. Másodszor, felfigyeltek arra, hogy a hurkok látszólagos mérete csökken azzal párhuzamosan, ahogy a keringési idô a Marsétól a Jupiterén át a Szaturnuszéig növekszik.
A fô epiciklusokat érintô két megfigyelést kiegészíthetjük egy harmadik, a Föld körül keringô bolygók és a Nap keringési pályájának méretére vonatkozó széleskörûen elterjedt spekulatív elgondolással. Hogy némi fogalmat alkothassunk ezen elgondolás alapjáról, tételezzük fel, hogy e pályájukon keringô testek mindegyike azonos sebességgel mozog, vagyis keringési idejük pályájuk sugarától függôen változik. Eszerint a Szaturnusz pályája lesz a legnagyobb, a Jupiteré kisebb, a Marsé pedig még kisebb. Ennek következményeire késôbb visszatérünk.
 |
| 5. ábra |
Eddig a ptolemaioszi rendszer kopernikuszi fogalmakba való átültetését a Kopernikusz által ismert három külsô bolygó példáján mutattam meg, most pedig a két belsô bolygóról, a Vénuszról és a Merkúrról kell szólnom. A belsô bolygók esetében az 1. ábra fordítottan érvényes. Az epiciklus a bolygó keringési ideje, a deferens pedig a bolygó kitérésének, vagyis a Föld Nap körüli éves keringésébôl fakadó látszólagos mozgásának ideje lesz. Azt találjuk ugyanis, hogy a Vénusz és a Merkúr kitéréseinek amplitudója beleillik a külsô bolygók adta sorozatba, következésképpen a Vénusz távolsága a Naptól a számítás szerint kisebb lesz, mint a Marsé, a Merkúré pedig kisebb, mint a Vénuszé. Így a ptolemaioszi rendszer mindhárom vonása érvényesnek bizonyult a belsô bolygókra is, amennyiben deferenseiket a külsô bolygók epiciklusainak feleltetjük meg.
Ezeket a megfontolásokat a modern tudós szemével nézve azt mondhatnám, hogy az új elmélet legszembetûnôbb eredménye ama különös tény magyarázata volt, hogy a hurkok megtételének megfigyelt idôtartama minden bolygó esetében azonosnak mutatkozott, azaz egy földi évet tett ki. De ez az egybeesés csak azért tûnik különösnek számunkra, mert nem tudunk mechanikai magyarázatot adni rá. Kopernikusznak fogalma sem volt arról, hogy a bolygók mozgásai mechanikai okokkal magyarázhatók, ezért aztán ezen egybeesések magyarázatát, amit mai fejjel a gondolkodás diadalának tekintünk, nem tartotta különösen nagyra. Számunkra az a tény, hogy a kopernikuszi rendszer szükségtelenné teszi azokat a fô epiciklusokat, melyekkel Ptolemaiosz a bolygók által tett kitérôket magyarázta, önmagában is nagy teljesítmény. Kopernikusz viszont ezt külön nem emeli ki, bizonyára azért, mert rendszerének más pontjain maga sem idegenkedett az epiciklusok használatától.
A mai tudósok fontos eredménynek tartják, hogy a kopernikuszi rendszer kiszámíthatóvá tette a bolygók keringési pályájának sugarai közötti viszonyulásokat. Kopernikusz azonban ezt jobbára a bolygótávolságok sorozatával hozza összefüggésbe, melyet egy hibás elméletbôl származtat.
E sorozatról felállított elméletét a De Revolutionibus I. könyve 10. fejezetének két passzusában fogalmazza meg, az egyik a fejezet elején található, a másik késôbb. Elôször a késôbbi passzust idézem, mivel ez jóval egyértelmûbb.
Quapropter prima ratione salve manente, nemo enim conventiorem allegabit, quam ut magnitudinem orbium multitudo temporis metiatur, ordo spaerum sequitur in hunc modum a summo capiens initium... (De Revolutionibus, szerk. Thoruni 1873, L. Prowe, E. de Losson, Boethke, Hagemann, 28. o.)Ami lefordítva a következôt jelenti:
Eszerint, amennyiben az elsô törvény helytálló – mivel nem valószínû, hogy bárki jobbat vessen föl, mint hogy a keringési pályák magyságát az idô nagyságával mérjük meg – a bolygók rendje a következô lesz...Ha azt mondjuk, hogy a sugarakat az "idô nagyságával mérjük meg", akkor azt állítjuk, hogy valamennyi bolygó egyenes vonalú sebessége azonos.[7] A fejezet eléjén olvasható szavak ezt erôsítik meg.
[C.G. Wallis: Great Books of the Western World, vol. 16, Chicago (1952)].
Errantium vero seriem penes revolutionum suarum magnitudinem accipere voluisse priscos philosophos videmus, assumpta ratione, quod aequali celeritate delatorum, quae longius distant, tardius ferri videntur, ut apud Euclidem in Opticis demonstratur.Kopernikuszt örömmel tölti el, hogy a bolygók általa kiszámított sorrendje egybevág az egyenes vonalú sebességek egyenlôségébôl származó törvénnyel. De természetesen ugyanezt a sorrendet kapjuk Kepler harmadik törvénye alapján is, mely szerint a keringési idôk négyzetei úgy aránylanak egymáshoz, mint sugaruk, vagyis közepes naptávolságuk, köbei. Az az összefüggés, amelybôl Kopernikusz a bolygók sorrendjére következtetett, merôben téves volt. Elképzelhetô, hogy nem vette észre ezt a hibát? Én azt hiszem, tisztában volt tévedésével.Az "aequali celeritate delatorum"-ot, vagyis az "azonos sebességgel mozgó tárgyak"-at értelmezhetnénk Euklidész hipotetikus állításaként is, de a bolygók késôbbi leírását tekintetbe véve úgy tûnik, hogy inkább ez a leírás adja meg jelentését.
A Commentariolusban, mely évekkel a De Revolutionibus elôtt született, Kopernikusz a három külsô bolygó relatív naptávolságát (sugarát) a következôképpen számítja ki:
A Szaturnusz deferense 30 év alatt tesz meg egy kört, a Jupiteré 12 év, a Marsé pedig 29 hónap alatt; olyan ez, mintha a körök mérete fékezné a körforgást. Ha ugyanis a nagy kör sugarát 25 részre osztjuk, a Mars deferensének sugara 38 rész, a Jupiteré 130 1/5, a Szaturnuszé pedig 230 1/6 rész lesz. A 'deferens sugarán'a deferens középpontja és az elsô epiciklus középpontja közötti távolságot értem. (Three Copernican Treaties, fordította és bevezette E.Rose, 2. kiadás, Dover Publications, New York, 74. o. A "nagy kör" a Föld keringési pályáját jelenti.)A 230 1/6:130 1/5:38:25 arányai 2%-on belüli eltéréssel kielégítik Kepler harmadik törvényét, de nagyban eltérnek a megfelelô keringési idôk – 29.5:12:2:1 – arányaitól. A Szaturnusz és a Föld aránypárjainak, vagyis a 230 1/6:25 és a 29.5:1 arányoknak az összevetésekor, csaknem háromszoros eltérést kapunk, ha pedig a Merkúrt is idevesszük, az arányok eltérése csaknem ötszörös lesz. Így vélem, az aránypárok ezen eltérésére gondolt Kopernikusz, mikor azt írta, hogy "olyan ez, mintha a körök mérete fékezné a körforgást". Ennek a fékezésnek például csaknem ötödére kellett volna csökkentenie a Szaturnusz sebességének Kopernikusz által magadott értékét ahhoz, hogy valóságos sebessége megegyezzen a Merkúr megfigyelt sebességével. Ez nem kerülhette el Kopernikusz figyelmét.
Ez a hiba, úgy tûnik, észrevétlen maradt, legalábbis a tudománytörténeti irodalomban nem találkoztam említésével. Sejtésem szerint, melyet ezzel a példával szeretnék alátámasztani, Kopernikusz azért tekintett el ettôl az eltéréstôl, mert csupán pontatlan elképzelései voltak a égbolt fizikai méreteirôl, és csak még pontatlanabbá váltak volna, ha ezzel az eltéréssel is számolnia kell. Mindezek fényében pedig a Kopernikusz által becsült naptávolságok nem lehettek számára olyan meggyôzôek, mint a modern tudósok számára, akik viszont a kopernikuszi rendszer többi elemének jó részét puszta fikciónak tekintik.
Mi gyôzte meg akkor Kopernikuszt saját rendszerének valóságosságáról? Ezt egyetlen mondatban összefoglalhatjuk. Sikerült megmagyaráznia a bolygók által rajzolt hurkokat egy olyan elmélet segítségével, mely a megfigyelt keringési idôket és a kitérések amplitudóit számításba véve megadja a keringési sugarak valószínû sorrendjét. Ez az eredmény volt az, ami megerôsítette Kopernikusz hitét harminc évig tartó vívódása közben s az ellenkezô véleményekkel szemben – és követôi erre hivatkozva állhattak ki a heliocentrikus rendszer valóságossága mellett.
Kopernikusz a III. Pál pápának ajánlott elôszavában azt írja, hogy végül felfedezte,
hogy ha a többi bolygó mozgását összefüggésbe hozzuk a Föld keringésével, és tekintetbe vesszük ennek az egyes bolygók keringési pályához viszonyított arányát, akkor nemcsak erre a jelenségcsoportra vetül rögtön fény, de a csillagok és szférák összeségének, sôt magának az égboltnak rendje és kiterjedése is olyannyira egybe fog vágni, hogy egyetlen elemét sem lehet többé elmozdítani anélkül, hogy zavart ne okoznánk a többi részletben és az univerzum egészében.Végre minden egybevág, mondja, és ez a rendszer valóságosságának jele.[8]
De miért váltott ki ez az állítása oly nagy tiltakozást kortársai, különösen a papság körében? Az ellenvetést elsôsorban nem a Biblia, hanem a papok és a világi tudósok által akkor már háromszáz éve hirdetett középkori filozófia védelmében fogalmazták meg. Az a filozófiai nézet, amelyet az egyházi emberek Osiandertôl Bellarmine-ig ívelô sora mellett olyan világi tudósok is védelmükbe vettek, mint Melanchton, Arisztotelészhez vezethetô vissza. Eszerint a világegyetem valamennyi lényegi tulajdonsága szükségszerû elsô elvekbôl vezethetô le; az univerzum tökéletességébôl következik például, hogy minden égitest egyenletes körmozgást végez. Ez a nézet kizárta annak lehetôségét, hogy a természet valamely lényegi tulajdonságát a csillagász empirikus megfigyelésekre támaszkodva fedezhesse fel; a csillagászati megfigyelésekre támaszkodó elméleteket puszta számítási segédeszköznek tekintették, s ez a ptolemaioszi rendszerre ugyanúgy vonatkozott, mint Kopernikusz rendszerére. Egyedül a filozófia volt alkalmas arra, hogy eljusson a természet lényegi valóságának megértéséig.
 |
| 6. ábra |
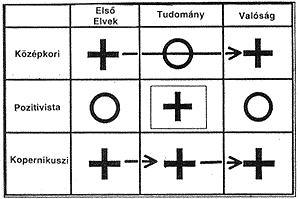
A kopernikuszi felfogás elleni ezen két támadás, a középkori és a pozitivista, illetve Kopernikusz saját álláspontjának jellemzését szolgálja a 6. ábra.
(1) A középkori álláspont szerint az elsô elvek közvetlenül fejtik ki hatásukat a valóságra, miközben a tudományra nincs efféle hatásuk. (2) A pozitivista irányzat egyrészt elválasztja a tudományt mindenféle tudományon kívüli elsô elvtôl, másrészt pedig a valóságtól, mivel ezek egyike sem ragadható meg. A tudomány, mely szerintük pusztán az adott tények hasznos összefoglalására való, nem hagyatkozik semmi önmagán kívüli dologra. (3) Végül a kopernikuszi hagyomány az alapvetô elveket az empirikus tudomány közvetítésével alkalmazza a valóság feltárására.
Kopernikusz nem kérdôjelezte meg a filozófia illetékeségét abban, hogy a dolgok lényegére vonatkozó szükségszerû következtetéseket vonjon le. Amikor Osiander emlékezetébe idézte, hogy asztronómiai elgondolásai nem adnak magyarázatot az égitestek mozgására[9], Kopernikusz alighanem egyetértett vele abban, hogy e mozgásokra csak az elsô elvek adhatnak magyarázatot, az ô asztronómiája nem. Kitartó ragaszkodása az égitestek egyenletes körmozgásának elképzeléséhez, ami rendszerét rendkívül bonyolulttá és nehézkessé tette, lényegében arisztoteliánusnak mutatja. Saját rendszerének víziója azonban azt sugallta számára, hogy az égi rend ezen konkrét tulajdonsága, noha alapvetôen a tapasztalatból származtatta, igaz és valóságos. Ekképpen állhatott ki elsôként ama metafizikai kijelentés mellett, hogy a tudomány képes új ismereteket nyújtani a lényegi valóságról, s állításának ekképpen szerezhetett érvényt a kopernikuszi forradalom.
A valóság tudományos megismerésének ezen lehetôségét tagadta tehát korunkban a pozitivizmus, és ugyanez a manapság széleskörûen kétségbe vont metafizikai igény az, amit vissza szeretnék állítani jogaiba.
1. Ernst Mach: Die Mechanik in ihrer Entwicklung (1883).
2. Henri Poincaré: Science et Hypothese, Paris (1902, 140-141, (Magyarul: Tudomány és feltevés, 1908) és Henri Poincaré: La Valeur de La Science, Paris (1914), 271-4. (Magyarul: A tudomány értéke, 1925).
3. Lásd alább a 12. jegyzetet.
4. Albert Einstein a "Biographical Notes"-ban, in Albert Einstein Philosopher-Scientist, szerk. P.A. Schlipp, New York (1949), 49. o. (Magyarul: Önéletrajz, in Albert Einstein: Válogatott tanulmányok, Bp. 1971. 288-289. o.), így ír Ostwaldról és Machról: "E kutatóknak az atomelmélettõl való idegenkedését kétségkívül pozitivista filozófiai beállítottságuk okozta. Érdekes példa ez arra, hogy a filozófiai elõítéletek a merész gondolkodású és finom ösztönû kutatókat is megakadályozhatják a tények értelmezésében. Az elõítélet – amely azóta sem halt ki távolról sem – az a meggyõzõdés, hogy tudományos ismereteket kizárólag tények szolgáltathatnak és kell hogy szolgáltassanak, szabad fogalomalkotás nélkül."
5. Alexander Koyré, "Les Origines de la Science Moderne", (Diogene, October 1956, no. 16.) címû írásában támadja a pozitivistákat azért, mert tagadják a tudományos ismeret valóságtartalmát.
6. Ezzel kapcsolatos kérdésemre S. Sambursky, a jeruzsálemi Zsidó Egyetem professzora a következõket írta: "Az Almagest valóban említi a bolygók epiciklikus hurkainak és ezek amplitudójának fontosabb adatait (IX. Kenyv, 3. fej., illetve XII. Kenyv), de Ptolemaiosz természetesen nem értelmezi ezeket az adatokat, és számszerû viszonyaik számára pusztán véletlenszerûek." Ezen összefüggéssel Rheticus kétségkívül számol az Oratio Primában (1540), a De Revolutionibusban azonban nem találtam nyomát.
7. F. Dobson and S. Brodetsky kiadása (Nicolaus Copernicus, De Revolutionibus, Elõszó és I. könyv, Roy. Aston. Soc. 1947) a "prima ratione salve manente" szövegrészt "a fentebb kifejtettek értelmében"-nek fordítja, ami jobbnak tûnik, mint az "amennyiben az elsõ törvény helytálló". A "quam ut magnitudinem orbium multitudo temporis metiatur" szavakat "hogy a keringési idõk a keringési pályák méretével arányosak"-ként adják vissza, ami talán túlságosan szabad fordítás, még ha lényegét tekintve helyes is.
8. "Így tehát a Föld mozgása magyarázatot ad arra, miért hajlik el látszólag oly sok égitest az egyenletes mozgástól" – írta Kopernikusz a Commentariolusban. Azt, hogy a dolgok összefüggése valóságosságuk jele, Rheticus a következõ szavakkal fejezte ki a Narratio Primában: "Teremtõnk oly bölcs, hogy mûvei mindegyikének nem egy, hanem két, három, vagy gyakorta még több használata van."
9. A De Revolutionibus olvasónak
címzett elõszavában Osiander az mondja az égi
mozgásokról, hogy az asztronómus "...a valódi
okokat és mozgatórugókat semmi módon sem képes
felismerni".
| Következõ rész | Vissza a tartalomjegyzékhez |
| Polanyiana | 7. évfolyam,1– 2. szám, 1998
http://www.kfki.hu/chemonet/polanyi/ http://www.ch.bme.hu/chemonet/polanyi/ |