H.Z.

Válasz: Sain Márton Matematikatörténeti abc-jében a következõt olvashatjuk:

pi (p)
A jelölés a periféria=kerület; görög szó kezdôbetûje. A kör kerülete és átmérôjé közötti arányt jelenti. 1739-ben Euler javasolta, hogy ezt az arányszámot a görög p betûvel jelöljék.

Az egyiptomi Rhind papiruszon (i. e. 2000–1700) a kör területére a t = (d–d/9)² képlet szerinti utasítás található. Eszerint a p = 256/81 » 3,1605.

Ugyanakkor Mezopotámiában a p =3 vagy a p  » 3 1/8 = 3,125 lényegesen durvább közelítô értékeket használták.

Az indiai Szulvaszútrák kb. i. e. 500-ból p értékére két érdekes kifejezést adtak. Ezek a  és a
.
Más indiai mûvekben a p -t Ö10-nek vették.

Kínában az i. e. III-I. századokban a p -nek nagyon sokféle közelítô értékét használták (3, Ö10, 92/29, 142/45 stb.). A Han-dinasztia alatt (i. e. 206–i. sz. 25) elrendelték a mértékegységek egységésítését. Ezt a munkát Liu Ci (i. e. 50–i. sz. 23) csillagász hajtotta végre. Ekkor történt a matematika történetében az az egyedülálló eset, hogy törvény szabta meg
nemcsak a mértékegységeket, hanem a p -nek a mindenkire kötelezô 3,1547 értékét is. Liu Huj a III. században 192 oldalú szabályos sokszöggel és Cu Csung-cse pedig 12 288 és 24 576 oldalú szabályos sokszöggel közelítette meg a kör területét. Az utóbbi így nyerte a 3, 141 592 6 < p  < 3,141 592 7 becslést.

A görögök nagy matematikusa, Arkhimédész a körbe írt szabályos sokszögekkel közelítve azt találta, hogy

.

Ha a határok számtani közepét vesszük, akkor p  számára 3,1419-et kapunk.

Ptolemaiosz Almagestjében, a II. században p  »377/120 = 3,14 166. Ô trigonometrikus módszerrel számolt.

A hindu Árjabhata 500 körül a p  »3,1416-del számolt.

Al-Kási perzsa matematikus p  értékét tizenhat tizedesjegyre számította ki. A francia Viète p-t tíz tizedesjegyig határozta meg. Ludolph van Ceulen holland matematikus 35 tizedesjegyig számította ki p értékét. Ezért szokás a p-t Ludolph-féle számnak is nevezni.

Az elôbb említett Viète trigonometrikus alakban adta meg p értékét:

Bár nem Leibniz fedezte fel, de róla nevezték el a

sort.

Valószínû, hogy a felfedezés érdeme James Gregory skót matematikusé.

1669-ben Wallis skót matematikus szerint:

.
 

1706-ban Machin francia matematikus  p-hez gyorsan közelítô sora:

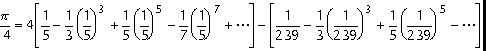
1784-ben Shancks angol matematikus e sor segítségével 707 tizedesjegyig számította ki  p értékét, körülbelül 30 évi munkával.

1944-ben Fergusson, ugyancsak angol matematikus kimutatta, hogy Shancks eredménye az 528. tizedestôl kezdve téves.

Elektronikus számológépekkel p-nek már több ezer jegyét kiszámították.

De Buffon gróf 1777-ben elsônek vezette be a geometriai valószínûség fogalmát a "tûprobléma" néven közismertté vált feladattal. Ez a feladat lehetôvé teszi a  p kísérleti meghatározását. Buffon példája szerint:

Vízszintes táblára d távolságú párhuzamos egyeneseket rajzolunk. Egy l< d hosszúságú tût dobáljunk a táblára irányítás nélkül. Mi a valószínûsége annak, hogy a tû valamelyik egyenesre esik? A keresett valószínûség értéke:

.

A zürichi Rudolf Wolf 1850-ben a képlet alapján kísérletileg meghatározta  p-t. Kísérletében d=45 mm és l=36 mm volt. 5000 dobás után  p értékére 3,1596-et talált.

A XVIII. században Lambert és Legendre bebizonyították, hogy  p irracionális szám.

1882-ben Lindemann német matematikus kimutatta, hogy  p transzcendens szám, azaz racionális együtthatójú algebrai egyenletnek gyöke nem lehet. Ez viszont azt jelenti, hogy  p euklideszi szerkesztéssel nem szerkeszthetô meg.