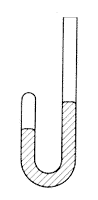
fizikában sokat sze-
replô "egyik végén
nyitott, másik végén
zárt U alakú csô".
Boyle – Hooke asz-
szisztenciája mellett –
kiterjedt kísérleteket
végzett vele
(Vákuum és légnyomás,
Simonyi Károly
"A fizika kultúrtörténete"
címû könyvébôl)
Két új kísérlet az összenyomott
és a kitágított levegõ rugóerejének
mérését illetõen
Részlet
A Defense of the Doctrine Touching the Spring and Weight of the Air,
3. kiadás, 1682
(Elsõ kiadás: 1660, második kiadás, amelyben
az alábbi beszámoló már szerepel: 1662)
(in: William Francis Magie: A Source Book in Physics, Harvard University Press, Cambridge, Massachusetts, 1963)
 |
| A mai középiskolás
fizikában sokat sze- replô "egyik végén nyitott, másik végén zárt U alakú csô". Boyle – Hooke asz- szisztenciája mellett – kiterjedt kísérleteket végzett vele (Vákuum és légnyomás,
|
Akkor nem tudtuk végrehajtani a próbát, mert a csõ alkalmasint eltörött. De mert az ilyenfajta pontos kísérlet igen fontos lenne a levegõ rugójára vonatkozó elmélet szempontjából, és (tudomásom szerint) senki sem végezte még el, s mert kivitelezése sokkal körülményesebb, mint gondolnánk, úgy a célnak megfelelõ hajlított csõ elkészítése, mint a domborodó higanyfelület valódi helyének pontos becslése miatt, feltételezésem szerint nem az olvasó kedve ellen való, ha megtudja, hogy néhány próbálkozás után ... végül készítettünk egy jókora csövet, amelynek a rövidebbik szárára erõsített papírcsíkot elõzõleg 12 hüvelykre és a negyedeire osztottuk, a hosszabbik szárán pedig több láb hosszú, ugyanilyen módon beosztott papírcsík volt. Ezután az üveg hajlított részét annyira töltöttük meg higannyal, hogy a felszíne mindkét szárban ugyanaddig a vízszintes vonalig érjen, s amint tanultuk, egyre több higanyt töltöttünk a hosszabbik szárba; majd gondosan megfigyeltük, milyen magasra emelkedett a higany a hosszabb csõben, amikor a rövidebb csõben valamelyik osztáshoz ért; ily módon több egymást követõ észlelést végeztünk, és az eredményeket lejegyezve a következõ táblázatot kaptuk:
A levegõ kondenzációjának táblázata
| A | A | B | C | D | E |
| 48 | 12 | 00 | 29 1/8 | 29 2/16 | 29 2/16 |
| 46 | 11 1/2 | 01 7/16 | 30 9/16 | 30 6/16 | |
| 44 | 11 | 0213/16 | 3115/16 | 3112/16 | |
| 42 | 10 1/2 | 04 6/16 | 33 8/16 | 33 1/7 | |
| 40 | 10 | 06 3/16 | 35 5/16 | 35 | |
| ... | ... | ... | ... | ... | ... |
| 16 | 4 | 58 2/16 | 8714/16 | 87 3/8 | |
| 15 | 3 3/4 | 6315/16 | 93 1/16 | 93 1/5 | |
| 14 | 3 1/2 | 71 5/16 | 100 7/16 | 99 6/7 | |
| 13 | 3 1/4 | 7811/16 | 10713/16 | 1077/13 | |
| 12 | 3 | 88 7/16 | 117 9/16 | 116 4/8 |
...AA. Azoknak az egyenlõ tereknek a száma a rövidebbik szárban, amelyek ugyanannyi, különbözõképpen kiterjedt levegõt tartalmaztak.
B. A hosszabbik szárban levõ higanyoszlop magassága, amely a levegõt az elõbbi méretre összenyomta.
C. Annak a higanyoszlopnak a magassága, amely a légkör nyomásával tartott egyensúlyt.
D. A B és C oszlop összege, amely a bezárt levegõ által elszenvedett nyomást mutatja.
E. Ekkora nyomásnak kell lennie ama a hipotézis szerint, amely feltételezi, hogy a nyomás és a kiterjedés egymással fordított arányban áll.
Bemutatandó, hogy nem szándék nélkül említettük meg a környezõ légköri oszlop súlyát a bezárt levegõ által fenntartott súly részeként, itt fûzzük hozzá az elõzõekhez, hogy amikor a csõ hosszabbik szárában a higanyoszlop körülbelül száz hüvelyk magas volt, egyikünk megszívta a nyitott csõvéget; ennek következtében (amint vártuk) a higany észrevehetõen felemelkedett a csõben. ... A környezõ levegõ nyomása részben csökkent, amint a levegõ a szívást végzõ kitágult mellkasába terjedt ki, ezért a bezárt levegõ szemmel láthatóan tágulhatott és a rá nehezedõ higanyt addig taszította, míg egyrészt az összenyomott levegõ erõs rugója, másrészt a magas higanyoszlop s a vele érintkezõ, kitágult levegõ közötti erõ egyenlõvé nem vált.
A levegõ összenyomására vonatkozó eredményeket a spontán kiterjedésére vonatkozó észlelésekkel egészítjük ki; így jobban kitûnik, hogy a higanyos kísérletek jelenségei milyen mértékben függenek a levegõ rugójának eltérõ erõsségétõl, amelyet a levegõ különbözõ fokú összenyomása és ernyedtsége szab meg.
A levegõ hígításának táblázata
| A | B | C | D | E |
| 1 | 00 | 29 3/4 | 29 3/4 | 29 3/4 |
| 1 1/2 | 10 5/8 | 19 1/8 | 19 5/6 | |
| 2 | 15 3/8 | 14 3/8 | 14 7/8 | |
| 3 | 20 2/8 | 9 4/8 | 915/12 | |
| 4 | 22 5/8 | 7 1/8 | 7 7/16 | |
| ... | ... | ... | ... | ... |
| 18 | 27 7/8 | 1 7/8 | 147/72 | |
| 20 | 28 0/0 | 1 6/8 | 1 9/80 | |
| 24 | 28 2/8 | 1 4/8 | 123/96 | |
| 28 | 28 3/8 | 1 3/8 | 1 1/16 | |
| 32 | 28 4/8 | 1 2/8 | 0 119/128 |
A. Azoknak az egyenlõ tereknek a száma a csõ tetején, amelyek ugyanannyi levegõt tartalmaztak.
B. Annak a higanyoszlopnak a magassága, amely a bezárt levegõ rugójával együtt egyensúlyban tartotta a légkör nyomását.
C. A légkör nyomása.
D. C és B különbsége, amely a bezárt levegõ által elszenvedett nyomást mutatja.
E. Ekkora nyomásnak kellene lennie a hipotézis szerint.
| Vissza | http://www.kfki.hu/chemonet/
http://www.ch.bme.hu/chemonet/ |