Körülbelöl tíz évvel ezelôtt egy módszert gondoltam ki a kapillaritási állandó megfigyelésére, mely lehetôvé tette a nyugvó folyadékok felületének teljes kiterjedésükben való vizsgálatát, és mely nekem ezért a kapillaritás-elmélet eredményeinek vizsgálatára különösen alkalmasnak látszott. Az utóbbi volt tulajdonképpen a cél, amire eredetileg törekedtem, de nemsokára vizsgálódásaim területe kibôvült: az elektrokapillaritás jelensége, az úgynevezett hatósugár kérdése merültek fel akaratlanul, és részben meg is oldódtak.

Közben sikerült a folyadékok felületi feszültségét tetszés szerinti idôtartamon át változatlanul tartanom, úgyhogy valódi értékeit biztosan meg tudtam állapítani. Ennek a legfôbb akadálynak az eltávolítása után, kiváltképpen Van der Waals úr kutatásai által ösztönözve, neki tudtam merészkedni e terület legfontosabb kérdésének, nevezetesen annak, hogy tanulmányozzam a felületi feszültség összefüggését a folyadék vegyi összetételével.

Habár eddigi kutatásaim legfontosabb eredményeit idôrôl idôre rövid közlemények formájában a Magyar Tudományos Akadémiának elôterjesztettem, mégis halogattam ezek részletes közlését, mert minden új eredmény újabb feladatokat is állított, melyeknek a megoldása számomra szintén kívánatosnak tûnt. Azonban a testek fizikai és kémiai tulajdonságai közötti összefüggésre vonatkozó összes kérdések iránti érdeklôdés, mely az utóbbi idôben egy sor gondos dolgozatot eredményezett, arra ösztönöz, hogy kutatásaim azon részét, mely kapcsolatban van ezzel a kérdéssel, kivonatban közöljem. Kutatásaimnak egy teljesebb kidolgozása késôbb kell következzék.
 
 

A kapillaritási állandó meghatározására 1875 óta használok egy módszert, melyet reflexiós módszernek fogok nevezni. Ez lényegében a következôkbôl áll. A folyadék FF felületére az S₁ és S₂ fényforrásokból kiinduló két sugárnyaláb, az S₁J₁  és S₂J₂ esik, amelyek ezen visszaverôdve egy katetométer vízszintesen beállított távcsövébe jutnak. A távcsô látómezejében két vízszintes fénycsík jelenik majd meg, amelyek az egyik, illetve a másik beesô fénynyalábból származó sugarakat vízszintes irányba verik vissza. A felület hajlását a J₁  és J₂ pontokban meghatározhatjuk a beesô sugarak irányából a mértani reflexiós törvény segítségével. Ezen pontok függôlegesen mért J₁P távolságát katetométerrel mérjük meg. Ezen, megfigyelés útján meghatározott mennyiségek segítségével, az elmélet által az illetô felületre megadott egyenletekbôl kiszámítható a kapillaritási állandó.

Magyarázatul szolgáljon a kapilláris hengerfelület példája, melyet egy folyadék egy nagyobb edény sík oldalfala mentén hoz létre. Az elmélet erre a következô egyenletet adja:

ahol a a kapillaritási állandó négyzetgyökét, z a nívófelülettôl lefelé mért függôleges ordinátáját jelöli, q pedig azt a szöget, melyet a felület normálisa a függôlegessel bezár. Ha z₁,q₁ és z₂,q₂-vel jelöljük a felület két pontjában ezeket a mennyiségeket, akkor a-ra a kövétkezô egyenletet kapjuk:

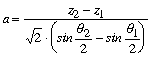
ahol a z₂–z₁, valamint a q₂ és q₁ értékeket is mérésekkel határozzuk meg.

Ezt az itt röviden körvonalazott módszert használtam mind a kapilláris hengerfelületek, mind a forgásfelületek esetében. A körülményektôl függôen a beesô sugarak irányát úgy választottam meg, hogy azok a folyadékon kívül vagy a folyadékban belül jussanak a felületre. A forgásfelületek esetében, amilyen a viszonylag kis átmérôjû csöveknél (körülbelöl 5–20 mm) keletkezik, ahol elmélet adta képlet nem áll rendelkezésünkre, az a mennyiséget olyan folyadékok segítségével, melyek kapillaritási állandóját már ismertem, összehasonlító mérésekkel határoztam meg.

Ezt a módszert egyes különleges vizsgálatokra megváltoztattam oly módon, hogy a katetométer helyett egy vízszintesen elmozdítható függôleges távcsövet használtam, és ezzel a két pont közötti vízszintes távolságot mérve, ezt az a állandó kiszámítására használtam.

Ennek a módszernek az elônyei a következôk:
1. Független az érintkezési szöget illetô bármilyen feltételezéstôl, akárcsak a szilárd edényfalak nedvesítésének jellegétôl is.
2. Ugyanennek a segítségével olyan folyadékokra is végezhettem méréseket, melyek lezárt üvegedényben, csak saját gôzeikkel érintkeznek. Ezáltal értem el a felületi feszültségnek egy alig sejtett állandóját, miáltal a kapilláris jelenségek megfigyelésének legnagyobb akadálya hárult el. A víz felületén végzett mérések ebben az edényben ugyanazon a hômérsékleten a kapilláris állandóra évek múltán is ugyanazt az értéket adták.
3. Ez a módszer lehetôvé tette a kapillaritási állandó változásának a figyelemmel követését olyan hômérsékleteken is, amelyek jóval felette vannak a folyadék forrpontjának, így például alkohol esetében 236 ^oC-ig, etiléter esetében 190 ^oC-ig. Ugyancsak lehetséges volt cseppfolyósodott gázok kapillaritási állandóját, így a szénsavét, a kénsavét és másokét meghatározni.
4. Az így nyert eredmények összehasonlítása a kapilláris csövek emelkedési magasságának megfigyelésébôl származókkal, felvilágosítást nyújtanak az illeszkedési szög nagyságát illetôen.
 
 

A különbözô testek fizikai és kémiai tulajdonságai az eddig több ízben megkísérlett módon, ti. ugyanazon, éspedig önkényesen választott hômérsékletek mellett nem hasonlíthatók össze, hanem csakis olyan különbözô hômérsékleteknél, melyek az összehasonlítandó testek mindegyikére a reája vonatkozó adatokból egyenkint meghatározandók.

Az összehasonlításnál követendô eljárást Van der Waals mutatta meg. A testeket ugyanis megfelelô állapotban, vagyis olyan abszolút hômérsékleteknél hasonlítja össze, melyek abszolút kritikus temperatúrájuknak egyenlô részeit teszik. Ámde a kritikus temperatúrák az ilyen vizsgálatoknál igen bizonytalan kiindulót képeznek, amennyiben nemcsak hogy nehezen határozhatók meg a megkívántató pontossággal, hanem még annak lehetôsége sincsen kizárva – sôt ellenkezõleg, egyes esetekben több mint valószinû –, hogy a test ennél a magas hômérsékletnél vegyi disszociációt szenved.

Eme nehézségeket kikerülendô, a megfelelô állapotnak másféle definícióját vettem alapul. Ugyanis részben (csepp)folyós, részben pedig telített gôzállapotban levô, vegyileg homogén testet egyenlô tömegû molekulákból álló rendszernek tekintve, ennek állapota molekuláinak térbeli elosztásmódjával jellemezhetô. Jelöljük tehát v-vel a folyadék molekulártérfogatát, vagyis annak a térnek átlagos értékét, melyet a molekula  a folyadékban elfoglal, u-val pedig ugyanezt  az adatot a telített gôzre vonatkozólag; akkor a v/u viszony a test állapotának jellemzésére alapul szolgálhat. Ha mármost ez a viszony két testre nézve a megfelelô T₁ és T₂ hômérsékletek mellett ugyanazon értékû, akkor a testek molekuláiból hasonló módon vannak összetéve. A hasonló összetétel ilyen állapotában a két testre

egyenlet érvényes, és a gáztérfogatokra vonatkozó tételek következtében

hol p₁ és p₂ a két test telített gôzeinek nyomását jelentik T₁ és T₂ hômérsékleteknél. Ezekbôl az egyenletekbôl kitetszik, hogy ekkor a testek a Van der Waals-féle definíció értelmében is megfelelô állapotban vannak.

Már most megkísérlettem egy bizonyos feltevésbôl következtetéseket vonni, abból a feltevésbôl ti., hogy a megfelelô állapotban, tehát a hasonló összetétel állapotában levô testek mechanikai értelemben is, azaz a megfelelô részeik között mûködô erôket és energiájukat illetôleg is hasonlók.

Ugyanis valamely folyadék felületének részét véve tekintetbe, melyet n molekula borít, a gõztôl reája gyakorolt nyomóerô

Másrészt a felületi feszültségnek megfelelô erô egy olyan vonal mentén, melyben m molekula sorakozik,

mely kifejezésben a₁ a felületi feszültséget, vagyis a hosszegységre vonatkozó energiát jelenti.

Képezzük ugyanezeket a kifejezéseket egy másik testnek ugyanazon számú molekulákból alkotott megfelelô részeire, ezek nyilván

Feltevésünkbôl az következik, hogy megfelelõ állapotokra vonatkozólag

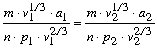
mibôl

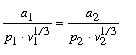
Hasonló okoskodást alkalmazva a megfelelô részek energiájára, a megegyezô állapotokra a következô kifejezést nyerjük:

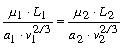
hol m₁ és m₂ a molekulár súlyokat, L₁ és L₂ pedig a gôzök lappangó hôit jelentik.

Eme tételek levezetésénél feltételeztem, hogy a folyadék és a gáz molekulái egyenlõ tömegûek. Azokat a folyadékokat, melyekre ez csakugyan áll, röviden összetetteknek fogom nevezni. Ezt az elnevezést behozva, az elôbb nyert tételek következôleg fogalmazhatók össze:

Ha bármilyen két egyszerûen összetett folyadékra T₁ és T₂ abszolút hômérsékleteik mellett
 

(1)

egyenlet áll, úgy ugyanezen hômérsékletek mellett még
 

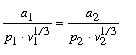(2)

és

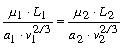(3)

egyenletek is érvényesek, továbbá (1) és (2)-bôl
 

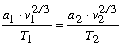(4)

és
 

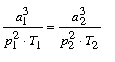(5)

A (3) alatti egyenlet egy tételt tartalmaz, melyet Waterston már 1858-ban, ámbár tökéletlenül – ti. tetszôleges hômérsékletekre – kimondott. Van der Waals is két erre vonatkozó tételt állított fel, melyek egyike az (5) egyenletben kifejezettôl csak annyiban különbözik, amennyiben abban a nyomás és a hômérséklet a kritikus állapotra van vonatkoztatva. Ez az utóbbi körülmény magyarázza meg, hogy miért nem sikerült e tétel helyességét igazolnia.

Ezáltal tévútra vezetve, eleinte én magam is más, a tapasztalatokkal jobban egyezô  összefüggést kerestem. A Magyar Tudományos Akadémiának 1885 elején benyújtott  értekezésemben mint tapasztalati tételt  mondtam ki azt, hogy a megfelelô hômérsékleteknél pT²/a³ kifejezés értéke különbözô anyagokra vonatkozólag megegyezik. E tételnek különösen vízre és az alkoholra vonatkozó értékei tényleg sokkal jobban megfelelnek. Elméleti tárgyalásaim jelenleg arra
indítanak, hogy a tételt visszavonjam, s utóbb ki fogom mutatni, mi okozza a víz és az alkohol sajátszerû magaviseletét.

A fönt levezetett összefüggésekbôl, nevezetesen a (4) egyenletben foglaltakból további következtetéseket is vontam, melyek a molekulártérfogat és a felületi feszültség között fennálló szoros és egyszerû kapcsolatot még világosabban feltüntetik.

Van der Waals okoskodásai szerint a test, mely T₁ és T₂ abszolút hômérsékletek alatt megegyezô állapotban van, ugyancsak megegyezô állapotokba jut, ha hômérsékleteik változása T₁ s illetôleg T₂-vel arányos. Megegyezô állapotokra tehát a (4) egyenlet értelmében

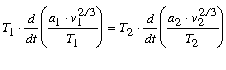
mibôl
 

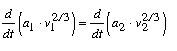(6)

következik. Ennek a hányadosnak értékét etiléterre vonatkozólag 0 ^oC-tól 190 ^oC közé esõ hõmérsékleti körben gondosan meghatároztam, s a hõmérséklettel való változást kimutatnom nem sikerült. Ámde ha ez egy testre áll, a (6) egyenlet folytán a megfelelõ hõmérsékleti határok között valamennyi más testre is ugyanannak kell állnia. Más testeken végzett megfigyelések kimutatták, hogy e hányadosok még tágabb hõmérsékleti határok között is állandók.

E szerint a következõ tételre jutottunk: A 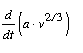hányados valmennyi egyszerûen összetett folyadékra állandó értékkel bír, mely a hômérséklettôl független, éspedig legalábbis abban a hômérsékleti körben, mely az abszolút nullpont és a kritikus temperatúra középhômérsékleténél magasabb. Állandóságról itt természetesen csak annyiban van szó, amennyiben az eddigi megfigyeléseim pontossága mellett megállapítható; nincs kizárva az az eset, hogy még pontosabb megfigyelések, nevezetesen a tágabb hômérsékleti határok között végzendô mérések ezen értéknek a hômérséklettôl való függését fogják kimutatni.

Az állandó értéke gyanánt, mint alább terjedelmesebben elôadom, 0,227-et nyertem. Ennek kiszámításánál v molekulártérfogatnak a molekulársúly és a sûrûség viszonyát vettem, s a felületi feszültség egységéül azt választottam, mely a folyadék felületében 1 mm-nyi hosszon a milligramm súlyával egyenlô erôt fejt ki. Ennek folytán

is írható, hol t azt a hômérsékletet jelenti, mely alatt a w^2/3 zérussal egyenlô. Megfigyeléseim, melyeket éter-, alkohol-, szénsav- és más folyadékokon végeztem, arra látszanak mutatni, hogy ez a hômérséklet a kritikus temperatúrával megegyezik, vagy legalább nem messze esik tôle.
 
 

A felsorolt tételek kísérleti igazolására igen gazdag anyag állott rendelkezésemre; nevezetesen 160 különbözô, részint szerves, részint pedig szervetlen anyagon végzett megfigyelések. Magam már régebben közzétett módszerem segélyével a folyadékok egész sorozatán meghatároztam a felületi feszültség értékét, s ezek között néhány cseppfolyósított gázét is; ezeken kívül R. Schiffnek a kapillaritási állandóra vonatkozó két értekezésében közölt eredményeit is felhasználtam. Ez utóbbiakat saját megfigyeléseimmel összehasonlítva, csak igen csekély eltéréseket találtam.

Az elsô kérdés az volt, hogy vajon a megfigyelések az olyan hômérsékletek alatt, melyeknél (2) alatti egyenlet áll, egyúttal a (3), (4), (5) és (6) egyenletek helyességét bizonyítják-e? A megegyezés néhány test, nevezetesen a víz, az alkoholok és a szénsavak kivételével, kielégítônek bizonyult; a felületi feszültséget a saját megfigyeléseimbôl, valamint R. Schiff elsô értekezésében* foglalt adatokból számítva, az eltérések az értéknek legfönnebb 5 százalékát érik el.

Ugyanezen szerzônek második értekezésébôl** vett adatok valamivel nagyobb eltéréseket mutatnak, mi könnyen megmagyarázható, minthogy ebben a kapillaritási állandó értékei a forrpontra vonatkozólag empirikus képletek segélyével, extrapoláció útján számíttattak ki.
Elmléleti fejtegtéseim fôeredmánye hasonlóképpen igaznak bizonyult. A 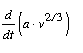hányados értékét gondosan meghatározva, a többi között a következõ adatokat nyertem:
 
 

Etiléter	6 oC-tól 62 oC-ig		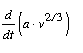= 0,228
Etiléter	62 oC-tól 120 oC-ig	"	= 0,226
Etiléter	120 oC-tól 190 oC-ig	"	= 0,221
Etilbromid	20 oC-tól 99 oC-ig	"	= 0,227
Etilbromid	99 oC-tól 213 oC-ig	"	= 0,232
Kloroform	20 oC-tól 60 oC-ig	"	= 0,230
Higanymetil	20 oC-tól 99 oC-ig	"	= 0,228
Szénoxiklorid	3 oC-tól 63 oC-ig	"	= 0,231
Széndioxid	3 oC-tól 31 oC-ig	"	= 0,228
Széndiszulfid	22 oC-tól 78 oC-ig	"	= 0,237
Kénessav	2 oC-tól 60 oC-ig	"	= 0,230

R. Schiff megfigyeléseinek adataiból számított értékek ezektôl 0,02-nél többel nem térnek el.

A fönt említett testek, név szerint a víz, az alkoholok és a szénsavak kivételt képeznek. Ezeket tüzetesebb vizsgálatnak vetettem alá; viselkedésük elméleti okoskodás útján azon feltevés segélyével fejthetô meg, hogy az illetô testek a vizsgálat alá esô hômérsékleti térben nem egyszerûen összetettek, azazhogy molekuláik cseppfolyós állapotban nem ugyanazon tömeggel bírnak, mint gôzállapotban. Ez vagy úgy lehetséges, hogy a folyadék olyan egyenlô molekulákból áll, melyek a gôzt alkotó molekulák egyenlô sokszorosai, vagy pedig hogy a folyadék olyan különféle molekulák keveréke, melyek a gôzmolekulák különbözô sokszorosai. Ámde ha valamely folyadéknál az elsô  eset áll, elôrelátható, hogy más hômérsékleti körbe való átmenetnél a második esetnek kell bekövetkeznie. Ha ti. az ilyen folyadék kritikus hômérsékletig hevíttetik, a folyadék molekuláinak okvetlenül gôzmolekulákká kell átalakulniuk, mivel hiszen ennél a hômérsékletnél egymással egyenlôkké  válnak.

A fizikai szétbomlás eme neménél, mely a vegyi disszociációtól jól megkülönböztetendô, még mindig lehetséges, hogy a folyadék összetett molekulái nagyobb hômérsékleti körön belül változatlanok maradnak, vagy pedig hogy szétbomlásuk hirtelen, talán éppen a kritikus temperatúránál megy végbe.

Az etilalkohol viselkedését vettem vizsgálat alá, éspedig egészen a kritikus hômérsékletig, s a következô eredményekre jutottam:
 

21 oC-tól 78 oC-ig		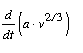= 0,104
78 oC-tól 180 oC-ig	"	= 0,136
108 oC-tól 138 oC-ig	"	= 0,159
138 oC-tól 168 oC-ig	"	= 0,183
168 oC-tól 199 oC-ig	"	= 0,202
199 oC-tól 236 oC-ig	"	= 0,226

E számok amellett látszanak tanúskodni, hogy eme folyadék molekulái alacsony hômérsékletnél összetettek, melegítés közben pedig folytonosan végbemenô bomlást szenvednek, mely bomlás 200 ^oC hômérséklet alatt véget ér, mivel ettôl a hômérséklettôl kezdve a hányados a gôzsûrûségbôl kiszámított molekulársúlynak normális értékét veszi fel.

A vízre vonatkozólag feltûnôen kicsiny értékek adódnak ki, ha számítás alapjául a H₂O képletet vesszük, tehát próbaképpen úgy számítottam a hányados értékét, hogy kettõs molekulákat tételeztem fel, s a következô eredményeket találtam:
 

3 oC-tól 40 oC-ig		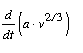= 0,159
40 oC-tól 100 oC-ig	"	= 0,180
100 oC-tól 150 oC-ig	"	= 0,228
150 oC-tól 210 oC-ig	"	= 0,227

Ennek értelmében a cseppfolyós víz molekulái 100 és 210 ^oC között a gáz kettõs molekuláival lenének egyenlõk, alacsonaybb hõmérsékletek alatt azonban még nagyobbak.

A 210 ^oC-t meghaladó hõmérsékletek mellett eddig még nem tehettem megfigyeléseket, mivel a víz ezen hõmérsékleteknél az azt elzáró üvegedény falait megtámadja.

A zsírsavak sorából különösen az ecetsavat vizsgáltam, és a C₂H₄O₄ képlet alapján a következõ értékeket nyertem:
 

21 oC-tól 107 oC-ig		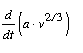= 0,132
107 oC-tól 160 oC-ig	"	= 0,132
160 oC-tól 230 oC-ig	"	= 0,138

De ha 2 C₂H₄O₄ képletet tesszük számításaink alapjává, a hányados értéke 0,211 lesz. Úgy látszik tehát, hogy az ecetsav molekulái ezen második képletnek felelnek meg, amit annak anomális gázsûrûsége csakugyan valószínûnek tüntet fel.

Még fölemlítem, hogy a higanyon is tettem méréseket, mégpedig 0 ^oC és 300 ^oC közé esô térben, s a hányados értékéül 0,18-at nyertem. Emellett azonban megjegyzendô, hogy itt a higany olyan hômérsékleti határok között vétetett megfigyelés alá, melyek kívül esnek ama határokon, melyek között tételemet érvényesnek mondtam ki.

Éter és széndiszulfid keveréket is tettem megfigyeléseim tárgyává, s azt tapasztaltam, hogy tételemet ezek is igazolják; molekulártérfogatul ez esetben  középértéket vettem, hol v₁, v₂  az egyes molekulártérfogatokat, k pedig a keverési viszonyt jelenti.

* Ueber die Capillaritätsconstanten der Flüssigkeiten bei ihrem Siedepunkte (Liebig's Ann. 1864, pag. 223 – Wied. Beibl. VIII. 457–461).
** R. Schiff: Ueber die Capillaritätsaequivalente der einfachen Körper (Wied. Beibl. 559–563).