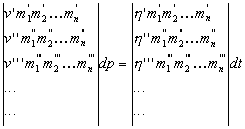
A heterogén rendszerek egyensúlyáról
Részlet
Transactions of the Connecticut Academy of Arts and Sciences,
3. k. 108–248, 353–524 (1875–1878)
in: Henry Marshall Leicester and Herbert S. Klickstein, A Source
Book in Chemistry 1400-1900, Harvard University
Press, 1963
Az anyag koegzisztens fázisairól
A komponensek tetszõleges halmazából képzõdõ,
különbözõ homogén testek vizsgálatához
célszerû bevezetni egy olyan kifejezést, amely csak
a testek összetételére és termodinamikai állapotára
vonatkozik, de mennyiségére vagy alakjára nem utal.
Ezeket az összetételükben vagy állapotukban különbözõ
testeket az anyag különbözõ fázisainak
nevezhetjük, és a mennyiségükben vagy alakjukban
különbözõ testeket ugyanazon fázis különbözõ
példáinak tekinthetjük. Azokat az egymástól
sík felülettel elválasztott, egymással olyan
egyensúlyt tartó fázisokat, amely egyensúly
nem függ a változással szembeni passzív ellenállástól,
koegzisztens
fázisoknak fogjuk nevezni.
Ha egy homogén test n, egymástól függetlenül változtatható komponensbõl áll, a test fázisa nyilván n+1 független változásra képes. Az r koegzisztens fázist tartalmazó rendszer, amelynek mindegyik fázisa ugyanabból az n, egymástól függetlenül változtatható komponensbõl áll, n+2–r fázisváltozásra képes. Hiszen a hõmérséklet, a nyomás és az aktuális komponensekhez tartozó potenciálok ugyanazt az értéket veszik fel a különbözõ fázisokban, és ezen mennyiségek változásai a (97)1 egyenlet értelmében annyi feltételnek tesznek eleget, ahány különbözõ fázis van. Ezért a fenti mennyiségekhez tartozó értékek független változásainak száma, vagyis a rendszert alkotó fázisok független változásainak száma, n+2–r.
Vagy, ha az r számú testnek nem ugyanannyi, egymástól függetlenül változtatható komponense van, de az r számú test, mint egész, függetlenül változtatható komponenseinek számát még mindig n-nel jelöljük, a rendszert alkotó fázisok független változásainak száma ekkor is n+2–r lesz. Ebben az esetben n-nél több komponens potenciálját kell figyelembe venni. Legyen a potenciálok száma n+h. A (97) egyenlet szerint r összefüggésünk lesz a hõmérséklet, a nyomás és az n+h potenciál változása között, valamint (43)2 és (51)3 szerint h összefüggésünk lesz ezek között a potenciálok között, s ezek alakja megegyezik azoknak az összefüggéseknek az alakjával, amelyek a különbözõ komponensek egységei között állnak fenn.
Ha tehát r=n+2, (az egymással továbbra is koegzisztens) fázisokban nem léphet fel változás. Nem tûnik valószínûnek, hogy r soha nem haladhatja n+2-t. Az n=1 és r=3 esetre példa a változatlan összetételû, tetszõleges anyag koegzisztens szilárd, folyékony és gáz alakja. Nem tûnik valószínûtlennek, hogy a kén és néhány egyszerû anyag esetében a koegzisztens fázisok egynél több triádja alakulhat ki, de teljesen valószínûtlen, hogy bármely egyszerû anyagnak négy koegzisztens fázisa legyen. Az n=2 és r=4 esetre példa az a vizes sóoldat, amely vízgõzzel és a só kétféle kristályával érintkezik.
Az n+1 koegzisztens fázis esete
Olyan differenciálegyenletet keresünk, amely n+1
koegzisztens fázisú rendszer esetén fejezi ki a hõmérséklet
és a nyomás változásai közötti összefüggést
(n továbbra is a rendszer, mint egész, egymástól
függetlenül változtatható komponenseinek a száma).
Ebben az esetben n+1 (97) általános alakú egyenletünk van (minden koegzisztens fázisra egy), amelyekben a különbözõ fázisokra vonatkozó n, v, m1, m2 stb. mennyiségeket vesszõvel különböztetjük meg. De t és p mindenütt ugyanazt az értéket veszi fel, és ugyanez érvényes m1, m2 stb. esetében is, ha ezek fellépnek a differenciálegyenletekben. Ha ezen potencálok teljes száma n+h, h független összefüggés lesz közöttük, ami megfelel annak, hogy azon komponensek egységei között is h független összefüggés van, amelyekre a potenciálok vonatkoznak, s így a (97) alakú egyenletekbõl kiküszöbölhetjük a potenciálok h változásait.
Legyen az egyik ilyen egyenlet
| v'dp=h'dt+ma'dma+mb'dmb+ stb. | (124) |
és a javasolt eliminációval a következõképpen
alakuljon át:
| v'dp=h'dt+A1'dm1+A2'dm2+ ... An'dmn | (125) |
Megfigyelhetõ, hogy például ma
a (124) egyenletben az Sa anyag esetében jelenti
a tömegéhez tartozó potenciált, és Sa
azonos
vagy különbözõ lehet az S1,
S2
stb. anyagoktól, amelyekre a (125) egyenlet potenciáljai
vonatkoznak. Miután a potenciálok közötti egyenletek,
amelyekkel az eliminációt végrehajtottuk, hasonlóak
a megfelelõ anyagok egységei közötti egyenletekhez
(hasonlítsuk össze a (38)4, (43)
és (51) összefüggést), ha ezeket az egységeket
Sa,
Sb
stb., S1,
S2
stb. szimbólummal jelöljük, a következõt kell
kapnunk:
| m'aSa+m'bSb+ stb. = A'1S1+A'2S2 ... A'nSn | (126) |
De ennek az egyenletnek az elsõ tagja (fajtáját
és mennyiségét tekintve) azt az anyagot jelenti a
testben, amelyre a (124) és (125) egyenlet vonatkozik. Mivel ugyanennek
fenn kell állnia a második tagra is, úgy tekinthetjük,
hogy ugyanaz a test az S1 anyag A1'
mennyiségébõl, az S2 anyag A2'
mennyiségébõl stb. áll. Ezért az általános
írásmódot követve (125)-ben m1',
m2'
stb.-t szerepeltetünk A1',
A2'
stb. helyett, s így:
| v'dp=h'dt+m1'dm1+m2'dm2 ... +mn'dmn | (127) |
De nem szabad elfelejtenünk, hogy azok a komponensek, amelyekre
az egyenletben az m1', m2' stb. vonatkozik,
nem szükségképpen független változók,
mint azok a komponensek, amelyekre a (97) és (129) egyenletben a
hasonló kifejezések vonatkoznak. Az n+1 egyenlet fennmaradó
része hasonló alakra egyszerûsíthetõ:
| v''dp=h''dt+m1''dm1+m2''dm2 ... +mn''dmn | (128) |
Ha az egyenletekbõl kiküszöböljük dm1, dm2, ... dm1a-t, a következõt kapjuk:
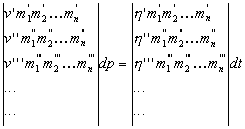 |
(129) |
Ebben az egyenletben v', v'' stb.-t egységnyinek tekintjük, ekkor m1', m2', m1'' stb. a különbözõ fázisokban levõ komponensek sûrûségeit jelenti, h', h'' stb. pedig az entrópiasûrûségeket.
Ha n=1,
| (m''v'–m'v'')dp=(m''h'–m'h'')dt | (130) |
vgy, ha m'=1 és m''=1, a szokásos
összefüggést kapjuk:
| (131) |
ahol Q az egységnyi anyag által elnyelt hõt jelenti, ha az anyag hõ- és nyomásváltozás nélkül megy át egyik állapotból a másikba.
Az n+1-nél kisebb számú koegzisztens fázisok
esetei
Ha n>1, és az összes S1, S2,
... Sn komponens mennyisége arányos két
koegzisztens fázisban, a fázisokra vonatkozó, két
(127) és (128) alakú egyenlet elegendõ az összes
potenciál változásainak kiküszöbölésére.
A két fázis koegzisztenciájának feltétele,
valamint az m1', m2', ... mn'
n–1
számú aránya és az m1'',
m2'',
... mn'' n–1 számú aránya
közötti egyenlõség feltétele elegendõ
arra, hogy p-t meghatározzuk t függvényében,
ha minden fázisra ismerjük a fundamentális egyenletet.
Ebben az esetben a differenciálegyenlet a (130) alakban írható
fel, ahol m' és m'' vagy valamelyik komponenes mennyiségeit,
vagy azokban a testekben levõ anyag teljes mennyiségeit jelenti,
amelyekre vonatkozik. A (131) egyenlet is érvényes ebben
az esetben, ha az anyag teljes mennyisége minden testben egységnyi.
De ez az eset különbözik az elõzõtõl,
mert az az anyag, amelyik a Q hõt felveszi az egyik állapotból
a másikba való átmenet során, és amelyikre
a képlet többi betûje vonatkozik, ugyan azonos mennyiségû,
de a különbözõ hõmérsékleteken
és nyomásokon általában nem azonos fajtájú.
Gyakran elõfordul, hogy az egyik fázis összetétele
lényegében változatlan, különösen,
ha kristályos testrõl van szó, és ekkor az
az anyag, amelyikre a (131) betûi vonatkoznak, nem változik
a hõmérséklet és a nyomás függvényében.
Ha n=2, két koegzisztens fázis, állandó hõmérsékleten, egyetlen fázisváltozásra is képes lehet. De minthogy (130) érvényes ebben az esetben, ha m1':m2'::m1'', m2'', állandó hõmérsékleten a nyomás általában maximumot vagy minimumot vesz fel, ha a két fázis összetétele megegyezik. Hasonlóan, a két koegzisztens fázis hõmérséklete általában maximumot vagy minimumot vesz fel állandó nyomáson, ha a két fázis összetétele azonos. Tehát a t és p szimultán értékeinek az a sora, amelynél a két koegzisztens fázis összetétele azonos, elkülöníti a t és p azon szimultán azon értékeit, amelyeknél nem lehetségesek koegzisztens fázisok, azoktól, amelyeknél két pár koegzisztens fázis léphet fel. Ez alkalmazható arra a folyadékra, amelynek két, egymástól függetlenül változtatható komponense érintkezik a folyadék gõzével vagy a folyadékban képzõdõ tetszõleges szilárd anyaggal.
Ha n=3, a három koegzisztens fázisra három
(127) alakú egyenletünk van, amelybõl a következõket
kapjuk:
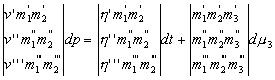 |
(132) |
Mármost az utolsó determináns értéke zérus, ha a három fázis egyikének összetétele a másik kettõbõl elõállítható. Ezért a három koegzisztens fázis nyomása általában minimumot vagy maximumot vesz fel állandó hõmérsékleten, és hõmérséklete minimális vagy maximális lesz állandó nyomáson, ha a koegzisztens fázisok összetételére vonatkozó fenti feltétel teljesül. A t és p szimultán értékeinek azon sora, amelynél a feltétel teljesül, elkülöníti a t és p azon szimultán értékeit, amelyeknél nem lehetséges három koegzisztens fázis, azoktól, amelyeknél a koegzisztens fázisok két triádja léphet fel. Ezek a meggondolások n nagyobb értékeire is kiterjeszthetõk, és n–2 különbözõ szilárd anyag olyan telített oldatainak forráspontjával és nyomásával illusztrálható, amelyek oldószereiben két, egymástól függetlenül változtatható komponens van.
| 1. (97) | –vdp+hdt+m1dm1+m2dm2 ... +mndmn=0 |
| 2. (43) | a1M1+a2M2+ ... +anMn=0
b1M1+b2M2+ ... +bnMn=0 stb., r egyenlet |
| 3. (51) |
| 4. (38) | a1S1+a2S2
... anSn=0
b1S1+b2S2 ... bnSn=0 stb., r egyenlet |
| Vissza |
http://www.ch.bme.hu/chemonet/ |