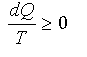...

Az egész mechanikai hôelmélet két fô tételen alapszik: a hô és a munka ekvivalenciáján és az átalakulások ekvivalenciáján.

Az elsô tétel analitikus kifejezése érdekében vegyünk egy tetszôleges, változó állapotú testet, és tekintsük azt a hômennyiséget, amelyet be kell fektetni ehhez az állapotváltozáshoz. Jelöljük ezt a hômennyiséget Q-val, és a test által leadott hôt tekintsük negatív abszorbeált hônek. Ekkor a végtelenül kis állapotváltozás közben elnyelt dQ hôt a következô egyenlet adja meg:

dQ = dU + AdW.

Ha a külsô munkát, az egyszerûség kedvéért, egyetlen betûvel jelöljük,

AW = w,

A második tétel legegyszerûbb analitikus kifejezéséhez tegyük fel, hogy a testet érintô változások körfolyamatot alkotnak, amelynek során a test végül visszatér eredeti állapotába. Ismét dQ jelenti az abszorbeált hôelemet, T a test az abszolút nullától számított hômérséklete a hôelem elnyelésének pillanatában, vagy – ha test különbözô részeinek hômérséklete eltérô – annak a résznek a hômérséklete, amely dQ-t elnyeli. Ha a hôelemet elosztjuk a megfelelô abszolút hômérséklettel, és az így kapott differenciált a teljes ciklusra integráljuk, akkor a következõt kapjuk:

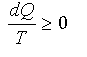(2)

ahol az egyenlôségjel azokra az esetekre vonatkozik, amikor a körfolyamatban lezajló összes változás megfordítható; a "nagyobb" jel a nem megfordítható változások esetén áll fenn.

Az a külsô munka (w), amelynek során a test az adott kezdeti állapotból egy másik állapotba jut, nemcsak a kiindulási és a végsô állapottól függ, hanem az átmenet módjától is.

A test U energiája ... egészen másként viselkedik. Adott kezdeti és végállapot meghatározza az energiaváltozást; tehát nem kell tudnunk, hogyan játszódott le a két állapot közötti változás, mert sem a változás lépései, sem a megfordíthatósága nem befolyásolja az energiaváltozást.

Ha – a (2) egyenlet szerint – a dQ/T integrál mindig zérus, amikor a test bármely kiindulási állapotból reverzibilisen tér vissza tetszôleges közbülsô állapotokon át a kiindulási állapotba, akkor a dQ/T integrál egy olyan mennyiség teljes differenciálja, amely csak a pillanatnyi állapottól függ, de nem függ attól, hogy a test miként jutott ebbe az állapotba. Jelöljük ezt a mennyiséget S-sel, ekkor dS = dQ/T , vagy ha az egyenletet bármely megfordítható folyamatra integráljuk, amelynek révén a test egy kiválasztott kezdeti állapotból elérheti jelenlegi állapotát, és S értékét a kiindulási állapotban S₀ jelöli:

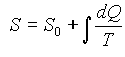
Ha S-nek megfelelô nevet akarunk adni, azt mondhatjuk, hogy S a test átalakulás-tartalma, ahogyan az U mennyiséget a test hô- és munkatartalmának nevezzük. Azt gondolom azonban, hogy a tudományos szempontból fontos mennyiségek nevét érdemesebb az ókori nyelvekbôl származtatni, hogy változtatás nélkül bekerülhessenek az összes modern nyelvbe, Ezért azt javasoltam, hogy az S mennyiséget – a görög h troph, átalakulás kifejezés alapján – nevezzük a test entrópiájának. Azért formáltam szándékosan ilyen alakúra az entrópia szót, hogy minél inkább hasonlítson az energia szóra, mert a két mennyiség, amelyet ezekkel a nevekkel jelölünk, fizikai fontosságát tekintve annyira közel áll egymáshoz, hogy jónak láttam, ha neveik is hasonlítanak némiképp egymásra.

...

Végül megengedhetem magamnak, hogy olyan témát érintsek, amelynek teljes tárgyalására nem ez a legalkalmasabb hely, mert a kifejtés túl hosszúra nyúlik, de azt hiszem, hogy a következô rövid összefoglalás sem lesz érdektelen, amennyiben hozzájárul azon mennyiségek fontosságának felismeréséhez, amelyeket a mechanikai hôelmélet második tételének megfogalmazásakor vezettem be. A második törvény [tétel] az általam megadott formában azt állítja, hogy minden átalakulás, amely a természetben lejátszódik, egy bizonyos értelemben, amelyet pozitívnak neveztem, magától, tehát ellentételezés nélkül játszódik le, de az ellenkezô, tehát negatív irányban is végbe mehet, ha egy idôben lejátszódó pozitív átalakulások kompenzálják. Ha ezt a törvényt a világegyetemre alkalmazzuk, arra a megállapításra jutunk, amelyre W. Thomson hívta fel elôször a figyelmet, s amelyrôl egy nemrégiben publikált dolgozatban már szóltam. Ez a megállapítás a következô: ha a világegyetemben zajló összes állapotváltozás közül az egyik irányban lejátszódó változások nagysága meghaladja a másik irányban lejátszódókét, akkor a világegyetem általános állapota egyre inkább az elôbbi irányban változik, és egy végállapot felé közeledik állandóan.

A kérdés most az, hogy ez a végállapot jellemezhetô-e egyszerû, de határozott módon. A feladat megoldható, ha az átalakulásokat – ahogy tettem – matematikai mennyiségekként kezeljük, amelyek ekvivalens értékei kiszámíthatók és algebrai összeadással egy összegben egyesíthetôk.

Eddig megjelent dolgozataimban végeztem ilyen számításokat a testekben jelen levô hôvel és a testek alkotórészeinek elrendezésével kapcsolatban. Minden test esetében két mennyiséggel kell számolni, hôtartalmának átalakulási értékével és felbomlásával; ezek összege az entrópia. Ezzel azonban nem zártuk le az ügyet. Figyelembe kell venni a sugárzó hôt is, másképp megfogalmazva azt a hôt, amely a világegyetemen keresztül az éter haladó rezgéseinek formájában terjed, valamint azokat a mozgásokat, amelyek nem férnek bele a hô fogalmába.

Ez utóbbi mozgások tárgyalása, amennyiben ponderábilis tömegek mozgásai, gyorsan elvégezhetô, hiszen egyszerûen levonható az alábbi következtetés: ha egy tömeg – amely akkora, hogy hozzá képest egy atom elenyészôen kicsinek tekinthetô – mint egész mozog, mozgásának átalakulási értékét ugyanígy elhanyagolható kicsinek kell tekinteni kinetikus energiájához képest. Ha tehát egy ilyen mozgást hôvé alakítunk át passzív ellenállás segítségével, az akkor fellépô, kompenzálatlan átalakulás ekvivalens értékét egyszerûen a keletkezô hô átalakulási értéke képviseli. A sugárzó hô azonban nem kezelhetô ilyen egyszerûen, mert egyelôre nem tudjuk, hogyan határozható meg az átalakulási értéke. Bár az elôzôleg említett új cikkben már tárgyaltam a sugárzó hô és a mechanikai hôelmélet kapcsolatát, nem érintettem az itt felmerülô kérdést, mert akkor csak azt akartam bizonyítani, hogy nincs ellentmondás a sugárzó hôre vonatkozó törvények és egy olyan alapvetô törvény között, amelyet a mechanikai hôelméletben feltételeztem. ...

Most csak egyetlen eredmény bejelentésére szorítkozom: azt a mennyiséget, amelyet egy testtel kapcsolatban a test entrópiájának neveztem, minden körülmény figyelembevételével terjesszük ki az egész világegyetemre, és ha ugyanezt elvégezzük az energia egyszerûbb fogalmával, a következô egyszerû formában fejezhetjük ki a világegyetem két alapvetô törvényét, amely megfelel a mechanikai hôelmélet két alaptörvényének [alaptételének]:

1. A világegyetem energiája állandó.
2. A világegyetem entrópiája maximum felé tart.