A 230 tércsoport fontosságát a kristályszerkezet meghatározásokban közel nyolcvan esztendeje (1919) P. Niggli ismerte fel. Azóta közel 38 ezer szervetlen és több mint 175 ezer szerves kristály szerkezetét publikálták. Ezek egyik legfontosabb adata a tércsoport. A szerves kristályok adatai a KKKI-ben 1979 óta elérhetô Cambridge Structural Database (CSD) archivált anyagából kérdezhetôk le. A több mint 174 ezer ellenôrzött szerkezetbôl statisztikát készítve kitûnt, hogy azok több mint 80%-a hat kis szimmetriájú triklin, monoklin. és rombos tércsoportban kristályosodik. Vezet a monoklin P2₁/c tércsoport 35%-kal. Ennek oka, hogy az alábbi molekula (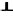) transzlációt

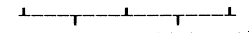
okozó 2₁ csavartengely szoros illeszkedésû molekula-paplanokat képez, amelyeket azután az inverzió 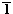 összetömöríti. E két, viszonylagos helyzetében a 2₁(0,Y,1/4) <–> 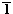(0,0,0) = c(X,1/4,Z) triplet által egymáshoz rendelt operátor automatikusan egy c csúszósíkot generál. A 2₁/c szimmetria pár dominanciája az említett hat tércsoport közül a C2/c-ben és a Pbca-ban is érvényesül. 1994-ben kimutattuk¹, hogy pszeudoszimmetria formájában P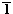 tércsoportú 8 molekulát tartalmazó triklin cellában (!) is megjelenik. 1997-ben megállapítottuk^2,3, hogy a CSD-ben több olyan triklin elemi cella van, melyben a 8 molekulát a 2*₁/c* pszeudoszimmetria pár kapcsolja össze. Felismertük, hogy ezek egy részében 2*₁ és c* topológiai viszonya megváltozik, ami szimmetria vándorlásban nyilvánul meg. E szimmetriák relatív migrációja (2n–1)1/8 koordináták megjelenése mellett jut egyensúlyba. Ezek kompenzálása egy új típusú, az 1884-tôl ismert 230 tércsoportban nem értelmezhetô q= 1/4 –> 3/4 –> 1/4 stb. aszimmetrikus transzlációval történik, amit az alábbi minta

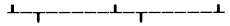
mutat be. Ez általánosan a 2_q(1/8,Y,1/4) <–> n_q(X_q,1/8,Z) = 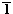(0,0,0) szimmetria triplettel írható le. A közelmúltban négy eltérô mértékben monoklinná transzformálható triklin kristályról három esetben (CIJSAP, DILFEJ, VARCOG) kimutattam, hogy a fenti triplet centrálás és az azt kísérô ortogonális tengely kialakulása mellett új, autonóm tércsoportként jelenik meg. További két ilyen "szabálytalan" tércsoport P2_q/c és P2₁/c_q vezethetô le, ha a fenti tripletben az 1/8 pozíciókat felváltva 1/4-re cseréljük. Az utóbbit a DIYMED-ben ismertük fel. E felismerés alapján a leggyakoribb 14. számú tércsoportból az alábbi szkémával leírt szimmetria eltolásokkal deduktíve is rendre eljuthatunk a pontcsoporttal azonos 10., illetve 11. és 13. tércsoporthoz.

E szimmetria vándorlásnak is felfogható három mûvelet felezôpontjaiban, azaz (2n–1)1/8 koordinátákkal alakulnak ki a helyesen átmenetinek nevezhetô szabálytalan tércsoportok. Ezek a klasszikus 230 tércsoportban nem értelmezhetôk, így a P2₁/c tércsoport degenerált (?) formáinak tekintendôk. Az aszimmetrikus transzlációk látványosak, így azután majdnem elfedik a lényegi változást. Ez pedig az, hogy bizonyos molekulák hagyományostól eltérô kristályosodásuk során a (2n–1)1/8 pozíciókban duplázott, de funkciójukban felezett szimmetria operátorokat alakítanak ki. Ezek nem ideális molekula formák esetében segíthetik az kedvezô szoros illeszkedés kialakulását.

Ez az elôadás a T023212 számú OTKA téma támogatásával készült.

1.) A. Kálmán and Gy. Argay: Analysis of non-crystallographic symmetries in the triclinic unit cell (P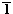, Z=8) of a 1,3-oxazepine derivative C₁₇H₂₂N₂O₃, Book of Abstracts, Fifteenth European Crystallographíc Meeting (ECM-15) p 223, Dresden, 1994.

2.) A. Kálmán and Gy. Argay: Description of pseudosymmetries in triclinic (P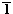) crystals with four molecules in the asymmetric unit. Book of Abstracts, Seventeenth European Crystallographic Meeting (ECM-17) p 125, Lisboa, 1997.

3 ) A. Kálmán and Gy. Argay: Topological description of pseudosymmetries in transcyclohexa[f ] -2,3,4,5,5a,9a-hexahydro-2 methyl-4-phenylaminocarbonyl-1,4oxazepin-3-one and other structures that crystallise in space group P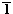 with Z=8. Acta Cryst., B (1998) közlés alatt.

4.) A. Kálmán: On the origin of transitional space groups in between triclinic and pseudo-monoclinic crystals. Submitted to the Eighteenth European Crystallographic Meeting (ECM-18), Prague, August 15-20, 1998.