MTA Kémiai Tudományok Osztálya
Felolvasóülés, 2013. március 19.
Lendvay György
MTA TTK AKI
Hogyan mozognak az atomok kémiai reakciók során?
Az
előadás kivonata (pdf)
***
Beszélgetés Lendvay Györggyel
A reakciódinamikai kutatás talán a magyar tudományos hagyományhoz is kötődik, hiszen Polányi Mihály már a kezdeteknél jelentős eredményeket ért el.
Valóban, Polányi Mihály ott volt a reakciódinamika születésénél, amikor az 1930-as években Németországban dolgozott. Ekkor a reakciókinetikát és a reakciódinamikát még nem különítették el egymástól. Polányi és munkatársai a vegyész számára egzotikusnak hangzó kísérletekre vállalkoztak: halogének és alkálifématomok reakcióit vizsgálták. Ezen nagyon csodálkoztam, amikor a reakciódinamika alapjairól tanultam az egyetemen, amíg rá nem jöttem, hogy miért folyamodtak ezekhez az anyagokhoz: ezek olyan reakciók, amelyek „hagyták magukat” tanulmányozni az akkori technikával. Azóta sokkal bonyolultabb kísérleti eljárásokat is kidolgoztak, ezért most már jóval szélesebb a tanulmányozható reakciók köre.
Mit vizsgáltak ezekben a rendszerekben?
Itt nagyon látványos jelenségek fordulnak elő: az alkálifématom már akkor „elkampóz” egy elektront a halogénmolekuláról, amikor a reaktánsok még messze vannak egymástól; ezt a lépést egy halogénatom átlépése követi. A reakcióban a kölcsönhatás típusától függően keletkezhetnek vibrációsan gerjesztett termékmolekulák is. Ezt a viselkedést harpooning mechanizmusnak, csáklyázásnak hívják. Polányi Mihálynak, aki az első elméleti reakciódinamikai vizsgálatokban is részt vett, nagy szerepe volt a jelenség modelljének kidolgozásában.
Polányi Mihály a lelke mélyén valószínűleg tudta azokat a szabályokat, amelyeket a fia, John Polanyi ötven évvel később számszerű eredmények birtokában fogalmazott meg. Az ifjabb Polanyi infravörös spektroszkópiai módszereket alkalmazott, és azt próbálta a mostanihoz képest még mindig meglehetősen kezdetleges technikákkal, egy spájz méretű laboratóriumban kitalálni, hogy milyen rezgési gerjesztettségű molekulák keletkeznek egyszerű reakciókban. Laboratóriumában a kísérletek mellett modellszámításokat is végeztek, amelyek elősegítették a kísérleti eredmények értelmezését. A Polanyi-szabályok néven ismert törvényszerűségek arról adnak információt, hogy mikor hatékonyabb a reakció előidézésére a rezgési és mikor a partnerek relatív kinetikus energiája; mikor keletkezik preferáltan vibrációsan gerjesztett, illetve „hideg” termékmolekula. Épp ezek a kérdések izgatták az idősebb Polányit is.
Arról, hogy a reakciókban a különböző szabadsági fokoknak mi a szerepe, más szóval a reakciók dinamikájáról részletes információkat lehet kapni a keresztezett molekulasugár technikával. Ezt módszert a Stern–Gerlach-féle kísérletből ismert Stern tanítványai és azok tanítványai fejlesztették tovább és használták először kémiai célokra. Közülük talán Herschbach volt a legsikeresebb. Az 1950-es, 60-as években még nem álltak rendelkezésre olyan jó minőségű anyagok, alkatrészek, mint ma. A sikeres kísérletekhez kellett egy kiváló műhely, amely elő tudta állítani a szükséges eszközöket. A kísérleti módszereket még ilyen nehézségek mellett is sikerült annyira hatékonnyá tenni, hogy a reakciók finom részleteiről sikerült látványos információkat szerezni. Ezt a kémikus és kémiai fizikus társadalom igen nagyra értékelte, s 1986-ban John Polanyi, valamint Dudley Herschbach és Yuan T. Lee kémiai Nobel-díjat kapott.
Polányi Mihály járatos volt már a kvantummechanikában?
A harmincas években Németországban „gyűltek össze” a kvantummechanikát kidolgozó fizikusok legjobb képviselői, és Polányi – aki akkor Berlinben volt professzor – szoros kapcsolatban állt velük. A születőben levő kvantummechanikát az 1930-as években kezdték alkalmazni a kémiai rendszerek leírására. Heitler, illetve London javasolt egy közelítést a hidrogénmolekula hullámfüggvényének megkeresésére. Erre épült aztán a Heitler, London, Slater, Pauling nevéhez kapcsolódó vegyértékkötés-elmélet. Polányi ismerte a hidrogénmolekula London-féle modelljét, és az akkor nála dolgozó Eyringgel kibővítette három hidrogénatomot tartalmazó rendszerre. A három atom együtt nem képez stabil molekulát, hanem közülük kettő hidrogénmolekulát alkot, és a harmadik hidrogénatom, ha közel kerül, ezt meg tudja támadni, s az egyik hidrogénatomot le tudja szakítani. Ez a legegyszerűbb kémiai reakció, amelyet akkortájt szintén magyar származású kutatók, a Farkas testvérek tanulmányoztak kísérleti módszerekkel. Amikor Polányi és Eyring a London által levezetett egyenleteket kiterjesztette a H3 rendszer kezelésére, a benne szereplő integrálokat nem lehetett hatékonyan kiszámítani, ezért helyettük kísérleti adatokból származtatható empirikus paramétereket építettek a modellbe. (Ez a módszer London–Eyring–Polányi, LEP néven vált ismertté). Ezzel lehetővé vált, hogy kiszámítsák a három hidrogénatom közt ható erőket meghatározó potenciális energiát nagyon sok olyan elrendeződésnél, amikor a három atom egy egyenesbe esik. Ezzel megalkották az első, kémiai reakciót jellemző potenciálisenergia-függvényt (mai szóval potenciálisenergia-felületet): ábrázolták az elektronok mozgásának LEP-módszerrel történő leírásából kapott energiát a H1–H2 és H2–H3 távolságok függvényében. Igen érdekes eredményt kaptak, némiképp a szerencsének is köszönhetően: az empirikus paramétereket jó érzékkel választották meg. Azt kapták, hogy a potenciálisenergia-felületen (röviden potenciálfelületen) a H1 + H2–H3 és a H1–H2 + H3 elrendeződéseknek megfelelő mélyedések között van egy nyeregpont. Más szóval a reaktánsokat a termékektől egy potenciálisenergia-gát választja el. Ez nagyon fontos eredmény: a kémián kívüli forrásból sikerült megmutatni, hogy mi az eredete annak az energiaküszöbnek, amelynek létezését Arrheniusnak kb. 50 évvel korábban fel kellett tételeznie, hogy meg tudja magyarázni, miért nő exponenciálisan a reakciók sebessége a hőmérséklet növelésével. A potenciálgát azóta központi fogalom a vegyészek gondolkodásában. Polányi és munkatársai nemcsak a potenciálfelület alakját mutatták meg, hanem tovább mentek: megpróbálták a reakció sebességét kiszámítani abból, hogy hogyan mozognak az atomok a potenciálfelület által megadott erők hatására. Az akkori számítástechnikai módszerekkel ez nem lett volna megoldható, ezért egy „analóg számítógépet” készítettek: agyagból megformázták a potenciálfelületet, és azon különböző helyzetekből, különböző sebességekkel golyókat gurítottak – így „integrálták” a klasszikus mechanikai mozgásegyenleteket. Ezzel a módszerrel próbálták megérteni, milyennek kell lenniük az ütközéseknek ahhoz, hogy reakció jöjjön létre.
A London–Eyring–Polányi-módszer továbbfejlesztett változata LEPS-módszer néven máig fennmaradt. (Azért kapta az S-t a neve végére, mert Shin Sato később beiktatott egy további empirikus paramétert, amitől az eredmények még jobbak lettek.) Néha most is használjuk a módszert, de nem azért, hogy az így kapható potenciálfelületet dinamikai számításokban felhasználjuk, hanem segédeszközként. Amikor potenciálfelületet illesztünk pontos ab initio számításokban kapott adatok alapján, akkor célszerű először egy LEPS-felületet kiszámítani, aminek az alakja kvalitatíve jó, és csak a különbség illesztését kell megoldani, ami jóval könnyebb feladat. Ez így sokkal hatékonyabb, mint amikor közvetlenül az ab initio pontokból indulunk ki.
Polányi Mihály 1933-ban Németországból átment Angliába, és ott még jó ideig foglalkozott reakciókinetikával. Eyring Berlinben volt Polányi posztdokja. Pár évvel később mind a ketten megpróbáltak módszert találni arra, hogy a potenciálgát magasságának ismeretében ki lehessen számítani a kémiai reakciók sebességi együtthatóját. Érdekes elolvasni azt a Faraday Transactions-számot, amelyben Polányi és Eyring egymástól függetlenül közli ugyanazt a módszert, amit ma átmeneti állapot elméletnek nevezünk (sokáig, Eyring nyomán, aktivált komplex elméletnek hívták). Ez volt az első „abszolút” reakciósebességi elmélet. Az „abszolút” jelző arra utal, hogy egy reakció sebességi együtthatóját, annak hőmérsékletfüggését mért sebességi adatok nélkül ki lehet számítani a módszerrel.
Polányi nemcsak reakciókinetikában alkotott maradandót, hanem a kémia egy sor más területén is. Mégis, talán a reakciókinetikában alkalmazható módszerek és elméletek kidolgozásával járult alapvetően hozzá a korszerű kémiai gondolkodásmód kialakításához. Hatása olyan nagy volt, hogy munkássága méltó lett volna a kémiai Nobel-díjra.
Mi különbözteti meg a reakciódinamikát a reakciókinetikától?
A reakciódinamika sokkal részletesebb képet ad a reakcióról, mint a reakciókinetika. Ha egy reakció dinamikájáról mindent tudunk, akkor a kinetikáját további információk nélkül jellemezni tudjuk. Az a különbség a kettő között, hogy a reakciókinetika olyan rendszerekkel foglalkozik, amelyek – amennyire csak lehet – termikus egyensúlyban vannak, pontosabban fizikai szempontból egyensúlyi rendszerek. Kémiai értelemben a rendszer nincsen egyensúlyban, hiszen a reakció azért játszódik le, hogy az egyensúly beállhasson. fizikai egyensúlyon azt kell érteni, hogy például az ütközések relatív kinetikus energiája megfelel a Maxwell–Boltzmann-eloszlásnak. A reakciódinamikában a kinetikával szemben „kivágunk egy szeletet” az eloszlásból, és kontrolláljuk az ütközési energiát, sőt, ha lehet, még a reaktánsok kvantumállapotát is. Bimolekulás reakciók dinamikai leírásakor nem a sebességi együtthatót, hanem a szórási hatáskeresztmetszetet határozzuk meg, sőt annak is a „kvantumállapotból kvantumállapotba” vezető folyamatokat jellemző változatait. Arra is kíváncsiak vagyunk, hogy mik a reaktánsokat, termékeket jellemző, vektor típusú mennyiségek – kezdeti és végső relatív sebesség, impulzusmomentum stb. – közti korrelációk. Ezek ismeretében keressük a kapcsolatot a potenciálfelület tulajdonságai és a reakció dinamikája között. Ilyen szabályszerűségeket tükröznek például a Polanyi-szabályok.
Ezek a szabályok már előbb is előkerültek: mit fogalmaznak meg?
John Polanyi és munkatársai rengeteg trajektória-számítást végeztek analitikus formulák segítségével kapott potenciálfelületeken. Többnyire a LEPS-módszerrel dolgoztak, amelyben változtatták a paraméterek értékét, és ezzel „tologatták” a potenciálgátat. Elsősorban azt vizsgálták, hogy mi határozza meg, hogy egy reakcióban keletkezik-e vibrációsan gerjesztett termékmolekula. Ezzel arra is választ kaptak, hogy mi előnyös a reakció lejátszódása szempontjából: a reaktánsok rezgési gerjesztése vagy az ütközési energia, más szóval a transzlációs hőmérséklet növelése. Ezeknek a számításoknak az eredményeiből szűrődött le például, hogy, ha korai a nyeregpont, akkor a rezgési gerjesztés hatástalan, mert nem fordítható a potenciálgát leküzdésére.
Mit jelent a „korai” kifejezés?
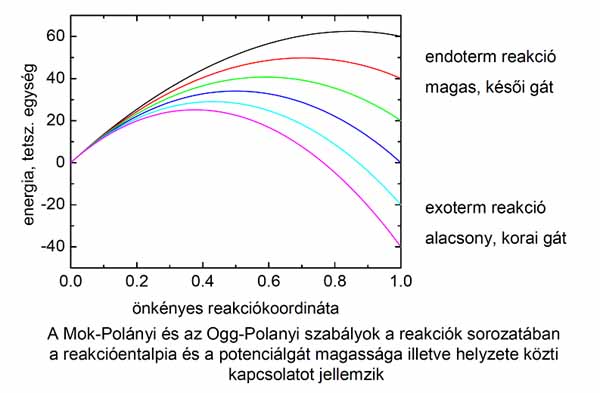
A nyeregpont helyzete a potenciálfelület alakjával kapcsolatos. Az, hogy a nyeregpont korai, azt jelenti, hogy a potenciálgát olyan atomelrendezésnél (szokásos kifejezéssel molekulageometriánál) van, amely a reaktáns(ok)hoz jobban hasonlít, mint a termék(ek)hez: a felszakadó kötés kevésbé nyúlt meg, mint amennyire a képződő kötés kialakult. A késői nyeregpont értelemszerűen „termékszerű” elrendeződésnél van, amelyben a reaktánsbeli kötés felszakadása és egyben a képződő kötés kialakulása előrehaladott állapotban van. Bimolekulás reakciók potenciálfelületének abban a metszetében, amikor az energiát a felszakadó és képződő kötés hosszának függvényében ábrázoljuk, a reaktánsoknak is, a termékeknek is egy-egy potenciálvölgy felel meg, ilyen ábrákat bemutattam az előadásomban. A potenciálgát e két völgyet választja el, rajta halad keresztül a minimális energiájú reakcióút. Ez utóbbi nem egyenes a fent említett két kötéshossz szerinti ábrázolásban, hanem egy, a rendszertől függően többé vagy kevésbé éles kanyarulata van abban a tartományban, ahol a felszakadó és a képződő kötés megnyúlása kb. ugyanakkora, de kicsi. A kanyarulat reaktánsoldalán a felszakadó kötés rövidebb, mint a képződő, a termékoldalon fordított a helyzet. Az, hogy a nyeregpont korai, illetve késői, azt jelenti, hogy a potenciálgát a kanyarulatnak a reaktáns-, illetve a termékoldalán van. A dinamikai effektusokat éppen a kanyar idézi elő. A jelenséget bobszán-effektusnak hívják. Ezzel az analógiával szokás szemléltetni a kémiai rendszer viselkedését, amiben a leglényegesebb, hogy az utóbbi, éppúgy, mint a bobszán, a pálya kanyarulatában, tehetetlensége miatt, „felmászik” a pontenciálfelület oldalfalára. A korai nyeregpont esetén az első feladat a gát megmászása, ezután következik a kanyaron való átjutás. Késői nyeregpont esetén viszont azokat a versenyzőket, akik át tudtak jutni a pálya (a reakcióút) kanyarulatán, emelkedő várja. Annak, hogy a reaktánsok számára mely szabadsági fokban biztosítjuk az energiát, a következő az analogonja a bob-pályán: a kis rezgési gerjesztettségnek az felel meg, hogy a szán a pálya kezdeti, egyenes szakaszán az árok alján halad, jobbra-balra kanyargása elhanyagolható. A nagy rezgési gerjesztettség analogonja az, hogy a szán már a pálya egyenes szakaszán erősen „kacsázik”, felváltva „felmászik” a pálya két oldalára. Azoknál a reakcióknál, amelyeknél késői a nyeregpont, az alacsony rezgési gerjesztettségű molekulát szimuláló szán a kanyarba érve felmászik a pálya oldalára, lelassul. Ha sikerül átkanyarodnia a termékcsatornába, ott egy emelkedő, a potenciálgát várja, amit csak kis eséllyel tud megmászni, mert a sebességének általában kicsi az a komponense, ami a gát megmászásához a legkedvezőbb. Ezért a szán nagy eséllyel visszacsúszik a pálya elejére, a reaktánsoknak megfelelő helyzetbe. Reakciódinamikai nyelvre fordítva ez azt jelenti, hogy a relatív kinetikus energia nem hatékony a késői nyeregpont leküzdése szempontjából. A reaktánsmolekula rezgési gerjesztése késői gát esetén azért előnyös, mert olyankor a gát reaktánsok felőli oldalán (abban a csatornában, amelyben a bobszán elindul) már eleve nagy amplitúdóval mozog a rendszer jobbra-balra, menet közben hol az árok egyik oldalára, hol a másikra mászik fel. Amikor a kanyarba ér, a rezgés tulajdonképpen a termékek szétválásának megfelelő mozgássá konvertálódik, a sebességvektora nagyjából éppen abba az irányba mutat, ahol a potenciálgát van, más szóval, elegendő kinetikus energia-komponense marad arra, hogy átjusson a gáton. Ennek az az analogonja a bobszán mozgásakor, hogy a versenyzők meg tudják oldani, hogy már a kanyar előtt jobbra-balra kanyarogjon a szán, és úgy időzítik, hogy amikor a jobbra irányuló kanyarulathoz érnek, a szán amúgy is jobbra kanyarodjon. Ekkor nem veszítenek energiát azzal, hogy a szán felmászik a pálya oldalfalára, és lendületből fel tud siklani a késői emelkedőn. Reakciódinamikai megfogalmazásban azt mondjuk, hogy a késői nyeregponton való átjutást a reaktánsok rezgési gerjesztése segíti elő. A Polanyi-szabályok arra is kiterjednek, hogy milyen formában (rezgési, forgási vagy transzlációs) szabadul fel a reakcióenergia. Fontos megjegyezni, hogy a bobszán-effektus miatt egészen más reakciósebességet kapunk, ha a potenciálgát korai,illetve késői, még akkor is, ha a gát magassága hajszálra pontosan megegyezik a két esetben.
John Polanyi és munkatársai a szabályokat háromatomos rendszerek vizsgálata alapján állapították meg. Az érvényességük csökken, ha több atom is van a rendszerben, de ha kvalitatív eltérést tapasztalunk a Polanyi-szabályok alapján várttól, akkor rendszerint megtaláljuk az okát, ami mindig a potenciálfelület jellegére vezethető vissza. Ilyen esetek a vibrációsan erősen gerjesztett molekulák reakciói, amelyeket az előadásomban is említettem.
A reakciók sorozatait vizsgálva John Polanyi édesapja nyomán azt is megállapította, hogy mely reakciók esetében vannak elsősorban korai gátak (az exotermek esetén), melyeknél későiek (főleg endoterm reakciók esetén). Így meg tudta magyarázni azokat a jelenségeket, amelyeket a méréseikben találtak.
Meddig terjednek ma a kvantummechanikai számítások?
A kvantummechanikát a vegyészek ma már rutinszerűen használják molekulák szerkezetének meghatározására. Itt a feladat mindig ugyanaz: az elektronok mozgását leíró Schrödinger-egyenletet kell megoldani, az atommagok helyzete rögzített, a molekula egyensúlyi szerkezetének pedig az az atommag-elrendeződés felel meg, amelynél a legalacsonyabb az energia. Ezt az eljárást szokás kvantumkémiának nevezni. A megoldandó Schrödinger-egyenlet formálisan mindig ugyanaz, és a megoldási algoritmusok függetlenek a molekula szerkezetétől, az atommagok és elektronok számától, ezért a feladat megoldására univerzális számítógépes programokat lehet kidolgozni. Számos olyan program készült, amely elvben bármekkora molekula szerkezetének kiszámítására alkalmas. Más a helyzet az atommagok mozgásának kvantummechanikai leírásával, ami a reakciók dinamikájának vizsgálatához szükséges. A magmozgás követése kvantummechanikai úton egyebek közt azért nehéz, mert minden rendszerre külön fel kell állítani a megfelelő egyenleteket, és ezeknek az egyenleteknek a megoldását is ki kell dolgozni. Most már elég nagy rutinra tett szert a szakma ezekben a számításokban. Van olyan program ebben a körben is, amely szinte univerzálisan működik, de csak az „atom + kétatomos molekula” rendszerekre. A sokatomos rendszerek reakciódinamikai kezelése viszont még nem megoldott. A legbonyolultabb rendszer, amelynek reakciódinamikai viselkedését jelenleg le lehet írni kvantummechanikai úton, a hat atomból álló „atom + metánmolekula” típusú rendszer, de valójában itt sem oldjuk meg a mozgásegyenleteket az összes szabadsági fokra. Az a módszer, amely a legtöbb szabadsági fokot explicite kezeli, négy szabadsági fokkal kevesebbet ír le, mint amennyi valójában van, úgy, hogy megkötéseket alkalmazunk (a három nem reagáló hidrogénatomot ekvivalensnek tekintjük, azonos C–H kötéshosszal és H–C–H kötésszögekkel). Az ilyen módszereket redukált dimenziós eljárásoknak nevezik. Ezeknek a jóságát nem lehet pontosan megállapítani, mert az összes szabadsági fok egzakt figyelembevételével kapható kvantummechanikai számításokat nem tudjuk kivitelezni. Éppen azon dolgozunk két munkatársammal, hogy kihasználjuk azt, hogy a kvantummechanikai modellel szemben klasszikus mechanikai úton könnyen lehet kezelni az összes szabadsági fokot. Az a célunk, hogy klasszikus mechanikai szinten megállapítsuk, mik a redukált dimenziós modellek gyenge pontjai. Ehhez megkeressük azokat a különbségeket, amelyek a teljes dimenziós klasszikus mechanikai számításban és a kvantummechanikai modellel analóg klasszikus mechanikai modellel kapott eredmények közt találhatók. Felhasználva, hogy a klasszikus és kvantummechanika ilyen rendszerekre legalábbis kvalitatíve – gyakran kvantitatíve – azonos eredményeket ad, a klasszikus mechanikai úton felderített „hibák” várhatóan a kvantummechanikai modellre is jellemzőek. Így meg tudjuk majd mondani, hogy milyen mértékű torzítást vezetünk be, amikor különböző megkötéseket alkalmazunk a kvantummechanikai egyenletek levezetésében. A klasszikus modell kidolgozásában, mint a kvantummechanikai esetben is, az egyenletek felállítása az igazi feladat, a megoldásukra jól bevált numerikus módszerek használhatók.
Mikor kell megválni a Born–Oppenheimer-közelítéstől, az atommagok és elektronok mozgásának szétválasztásától?
Amikor a vegyész reakciókról gondolkodik, az atomok a kölcsönható egységek, szemben a kvantumkémiával (ami valójában fizika), ahol az egységek az atommagok és az elektronok. Úgy képzeljük, hogy az atomok között erők hatnak, és ezt egy potenciálisenergia-függvény, a potenciálfelület adja meg. A vegyészi és a kvantumkémiai leírást a Born–Oppenheimer-közelítés köti össze, amely azon a feltételezésen alapszik, hogy az elektronok mozgása elválasztható az atommagok mozgásától. Kvalitatíve azt mondhatjuk, hogy, mivel az elektronok tömege sokkal kisebb a magokénál, sokkal gyorsabban mozognak azoknál, és mindig adaptálódnak a lassan mozgó atommagok által előidézett potenciáltérhez. Amikor a két mozgás szeparációjának feltételei teljesülnek, akkor az atommagok (amelyek az atomokat képviselik) mozgását meghatározó erőket az elektronmozgás Schrödinger-egyenletének megoldásával megkaphatjuk. Minden atommag-elrendeződésnél minden elektronállapothoz tartozik egy energia. Az elektronenergiák a magkoordináták függvényében egy-egy sokdimenziós felületet alkotnak, a különböző elektronállapotokhoz tartozó potenciálfelületeket.
A Born–Oppenheimer-közelítés akkor jó, ha az elektronállapotok energiái messze vannak egymástól. Ilyenkor azokban az egyenletekben, amelyeket a közelítés levezetéséhez felírunk, a csatolási tagok nagyon kicsik. Ha viszont a potenciálfelületek közel kerülnek egymáshoz, ezek a csatolási tagok nagyon nagyok lehetnek, és valójában fel kellene adnunk a potenciálfelület fogalmát. A rendszer elektronállapota tulajdonképpen nincsen jól definiálva ebben a tartományban. Viszont a potenciálfelület-képben annyira hatékonyan tudunk gondolkozni, hogy ilyen körülmények között is ezt használjuk. Azt mondjuk, hogy kereszteződnek a potenciálfelületek, és tudomásul vesszük, hogy egyik elektronállapotból átmehetünk a másikba.
A Born–Oppenheimer-közelítés nagyon sokszor jól működik a molekulák egyensúlyi elrendeződése környékén. Ez a vegyészek nagy szerencséje: molekulaszerkezeteket általában megbízhatóan lehet számítani a kvantumkémia bevált módszereivel. Ahogy mondtam az előadásban, a reakciókinetikában sokáig azt gondolták, amit a kvantumkémiában: átlagos esetben a Born–Oppenheimer-közelítés nagyon jó, és elég megismerni a legalacsonyabb energiájú állapot potenciálfelületét. A reakciók lejátszódása közben azonban a reagáló rendszer szükségszerűen eltávolodik az egyensúlyi geometriától, és egyre több reaktív rendszerről derül ki, hogy a potenciálfelületek bizony közel kerülnek egymáshoz. Sőt, akár kereszteződnek is. Ennek következtében a rendszer a reakció közben megváltoztathatja az elektronállapotát. Ezért manapság már nem jelentjük ki előre, hogy a rendszer azon a potenciálfelületen fogja befejezni a reakciót, amelyiken elindult, hanem sokkal óvatosabbak vagyunk. A számítási eljárások és a számítógépek teljesítménye újabban olyan mértékben fejlődött, hogy ésszerű idő alatt, ésszerű pontossággal ki lehet számítani a fent említett nemadiabatikus csatolási tagokat. Ezt kihasználva manapság a nemadiabatikus effektusok precíz kezelése divatos kutatási területté vált.
Újabb területnek tűnik a van der Waals-kölcsönhatások tanulmányozása.
Bármely két molekula között vannak van der Waals-kölcsönhatások, vonzó erők. A van der Waals-komplexek tulajdonságait tanulmányozni is lehet kellően alacsony hőmérsékleten: például néhány kelvines hőmérsékletet állítanak elő, ahol a molekula rezgései, forgásai gyakorlatilag „befagynak”, és a képződmény számos tulajdonságát megvizsgálják spektroszkópiai úton. van der Waals-komplex a reakcióra képes molekulák között is képződhet, amit a potenciálfelületek kiszámításakor is látunk. Ezeknek a kísérleti vizsgálata sokkal nehezebb. Az ilyen komplexek képződése azért fontos egy reakciókinetikus számára, mert a jelenségnek kinetikai, dinamikai következményei lehetnek. A van der Waals-komplexek reakciókinetikai szerepét jelenleg többé-kevésbé ad hoc módszerekkel kezelik. A statisztikus módszert, az átmeneti állapot elméletet alkalmazzák rájuk, ami azzal a feltételezéssel jár, hogy ha keletkezik egy ilyen komplex, akkor az energiája szabadon eloszlik a molekulában – így „el tudja felejteni”, hogyan képződött. Ez akkor igaz, ha mind a komplexet alkotó molekulákon belül, mind pedig közöttük gyors az energiaáramlás. Kis molekulák van der Waals komplexeiről tudjuk, hogy a belső és a külső szabadsági fokok között, vagyis a molekulán belüli és az intermolekuláris szabadsági fokok között gyenge a csatolás, az energiaáramlás lassú. Ilyen komplexekre nem teljesülnek a statisztikus módszer alkalmazhatóságának a feltételei. Sokatomos reakciópartnerekből felépülő van der Waals-komplexek esetén a csatolás nagyságát jelenleg kevéssé ismerjük. A közeljövőben azt szeretnénk megvizsgálni, milyen is ez a csatolás, valóban úgy reagál-e a komplexbe kapcsolódott reaktáns-pár, ahogyan a statisztikus módszer alkalmazásakor feltételezik. Emellett azt is szeretnénk megtudni, hogy mik a következményei annak, ha a van der Waals-komplex egy harmadik partnerrel ütközik, milyen nagyságú energiát nyer vagy veszít, és a viselkedése mennyire tér el egy jól definiált molekuláétól.
A legtöbb tudományban érvényesül az a tendencia, hogy a kutatók egyre mélyebbre látnak, egyre finomabb részleteket próbálnak feltárni.
Szerencse dolga is, hogy az ember mikor talál olyan effektust, amelynek mentén érdemes mélyre ásni. Nagyon tanulságosnak tartom azt a folyamatábrát, amelyet az előadáson megmutattam. A kísérletező felteszi a kérdést, az elméleti szakember megpróbálja leírni a jelenséget. Ha sikerül a kísérleti eredményeket reprodukálni, akkor az elmélet alapján javaslatot lehet tenni olyan kísérletre, amivel ellenőrizni lehet, hogy az elméleti úton kidolgozott modell alkalmas-e arra, hogy az ismert tények mellett a kísérletileg még nem tanulmányozott jelenségekről is megbízható információt nyújtson. Ha az újabb mérés eredménye egyezik a jósolttal, akkor az elmélet jó, és újabb jóslással újabb kísérletet lehet javasolni, ha pedig nem, akkor az elméleti modellben meg kell keresni azt az elhanyagolást (esetleg hibát), amit korrigálni kell, és így haladunk lépésről lépésre előre. Erre nagyon látványos példák vannak a reakciódinamikában.
Magyarországon is mérnek olyan finom effektusokat, amelyek „kölcsönhatásba léphetnek” az elmélettel?
Korszerű reakciódinamikai
berendezések nem állnak a vegyészek rendelkezésére Magyarországon. A legközelebbi
keresztezett molekulasugár-berendezések például Perugiában és Göttingenben
vannak. Más technikák helyettesíthetik ezt a módszert, de ezek is nagyon
drágák. Ha az embernek szerencsés külföldi kapcsolatai vannak, akkor az
ottani kísérletezőktől kaphat érdekes kérdéseket, amelyek megválaszolása
kihívást jelent. Eddig szerencsém volt.