MTA Kémiai Tudományok Osztálya
Felolvasóülés, 2012. március 20.
 

Császár Attila
ELTE Kémiai Intézet, Molekulaszerkezet és Dinamika Laboratórium, csaszar@chem.elte.hu
 

Egzotikus úti célok Kémiába
Az előadás kivonata: Létezik-e élet a molekulák számára a disszociációs határon túl? Mekkora az a legnagyobb gát, ami mögül még ki tud bújni egy molekula az abszolút zérus hőmérséklet közelében? Hányféle vízmolekula létezik, és mi a helyzet például az ammónia, illetve az izotóphelyettesített származékok esetében? Mennyire kiváló hálózatépítő a kvantummechanika? Valóban mindig úgy játszódnak le az elemi kémiai reakciók (pl. az SN2), mint ahogy a tankönyvekben szerepel? Van-e jelentősége a magspineknek a kémiában az NMR-spektroszkópián kívül? Megismerhető-e egy molekula teljes színképe? Mi vár a vegyészekre a Born–Oppenheimer-közelítésen túl, avagy függ-e a magok tömege azok távolságától? Lehet-e szerepe a kvantumelektrodinamikának (a Fizikából Kémiába tartó vonat (egyelőre) utolsó kocsijának) a kémiában? Ilyen és hasonló, talán nem is olyan egzotikus kérdések megválaszolását segítik elő a kvantumkémia negyedik korszakával kapcsolatos módszerfejlesztéseink (A. G. Császár et al., Phys. Chem. Chem. Phys. 2012, 14, 1085), melyek az előadás alapját képezik.

Az előadás diái
 
Beszélgetés Császár Attilával

Két éve, egy ünnepi előadáson a kvantumkémia harmadik, kvantitatív korszakáról beszélt, amely a kvalitatív és félkvantitatív periódusok után 1970 körül indult. A kvantitatív megközelítés, mondta, „megelőzheti, kiválthatja, kiegészítheti és okkal megkérdőjelezheti a kísérletet”. A mostani előadáson már egy negyedik korszakot definiált.

A kvantumkémia harmadik korszakának egyik legfőbb hirdetője H. F. Schaefer professzor volt, a Center for Computational Quantum Chemistry igazgatója a georgiai egyetemen (UGA, USA). Amikor a 90-es években gyakran együtt dolgoztunk, kérdezgettem, hogy meg tudja-e már mondani, mi lesz a negyedik korszak. Mindig nemmel válaszolt. Az ő tiszteletére rendeztek a berkeley-i egyetemen egy nagy érdeklődéssel kísért világkonferenciát 2010-ben, és azt gondoltam, hogy nekem itt a kvantumkémia negyedik korszakáról kellene beszélnem. Így is lett: a negyedik periódust a közel egzakt magmozgás-számításokhoz kötöttem – kiegészítve a kvantumkémia elektronszerkezet-számítással foglalkozó ágát a magmozgás-számításokkal foglalkozó ággal. A jelen lévő nagyszámú kvantumkémikus hallgatóság nem tiltakozott az új definíció ellen, sőt örömmel fogadta. Ennek hatására írtuk meg a kivonatban említett, a PCCP folyóirat szerkesztőjének felkérésére született review cikket, amelyben a módszerfejlesztéseinkről is beszámoltunk.

Megjegyzem, ha valaki elővesz egy hétköznapi „quantum chemistry” tankönyvet, csak az elektronszerkezet-számításról olvashat benne. A kvantumkémikusok többsége még ma is úgy tesz, mintha a molekuláris kvantumkémiában csak az elektronok mozgásával kellene foglalkozni. Talán ennek a szemléletmódnak a megváltozásához is hozzásegíthet ez az új definíció.

A régi szemlélethez talán alapot ad a Born–Oppenheimer-közelítés, amely a molekula hullámfüggvényét elektron- és magkomponensre választja szét.

Így van. Ez ugyanakkor nem jelentheti azt, hogy kizárólag az elektronok kvantummechanikai alapú mozgásával foglalkozzunk! Mi most azt mondjuk, hogy a magmozgásokat is meg kell vizsgálni a lehető legpontosabb módokon, és akkor nagyon sok érdekes, ma még egzotikusnak tekintett jelenség is tárgyalható lesz. Így válik teljessé az elméleti leírás.

Milyen feladatot ró ez a megközelítés a kvantumkémikusokra?

A magmozgás leírására használható matematikai apparátus hasonló ahhoz, mint ami az elektronok mozgásának leírására szolgál. De kellően különböző is, ezért nem véletlen, hogy sokkal lassabban fejlődött ki ez az ág.

Az elektronok megkülönböztethetetlenek, tehát a számításkor azonos részecskékkel kell dolgoznunk. A magok viszont különbözőek, az egyik szén, a másik nitrogén stb. A nehézségek egy részét a különböző részecskék kezelése jelenti. A magmozgások magas szintű számítása az 1970-es évek elején indult el. Az elektronszerkezet-számítás eddigre a harmadik korszakban tartott: már kvantitatív eredményeket tudott adni, ugyanakkor a magmozgást csak nagyon közelítően kívánták leírni. Amikor a molekulák elektronszerkezete érdekel bennünket, akkor a molekulának általában egy, legfeljebb néhány állapota érdekel bennünket. A magmozgás számítások esetén ugyanakkor sokszor ezer, vagy akár százezer állapotot kell számba vennünk, ami jelentős nehezítést jelent.

A tankönyveknek természetesen igazuk van abban, hogy a molekulák legtöbb tulajdonságának megértéséhez elsősorban az elektronok mozgásának leírása szükséges, de a finomabb részletek megismeréséhez már nem elhanyagolható a magok mozgásának nagyon pontos kezelése sem.

Nagyon fontos továbbá hangsúlyozni, hogy ha olyan területre érünk, ahol a kísérletek nem végezhetők el, akkor nem marad más a vegyész számára, mint a számítás, sokszor a kvantumkémiai számítás. És ha az elérhető kísérleti adatok alapján megállapítható, mennyire pontos az elméleti számításunk, akkor bízhatunk abban, hogy „a kísérleteken túl” is ugyanolyan pontosságot tudunk elérni, azaz ki tudjuk váltani a drága kísérleteket viszonylag olcsóbb számításokkal.

A már idézett előadásában azt mondta, hogy akkor érnek el nagyobb pontosságot, ha a kísérleti és az elméleti eredményeket egyfajta „iterációnak” vetik alá. Ez a kvantumkémiában mást jelent, mint más típusú kutatásokban?

Azt hiszem, nincs alapvető különbség, és azokban a körökben, ahol én is mozgok, elfogadott, hogy sem az elméletnek, sem a kísérletnek nincs prioritása, hanem a kettőnek együtt kell „a választ” megadnia. Néha a kísérlet tart kicsit előbbre, néha az elmélet, de ha tovább szeretnénk lépni, például egy mérnöki feladat megoldása vagy az üvegházhatás vizsgálata érdekében, akkor sehogy máshogy nem érdemes hozzálátnunk, mint a kísérlet és elmélet együttes figyelembevételével.

A feladat tehát az, hogy dolgozzuk föl a lehető legjobban a kísérleti adatokat, hogy mindenhol, ahol a primer kísérleti adat rendelkezésre áll, felhasználhassuk őket, és a „lyukakat” tömjük be az elméleti adatokkal ott, ahol valamilyen okból nem lehet kísérleti adatokat előállítani, vagy eddig még nincsenek.

A közelmúltban kifejlesztettünk egy módszert a rendkívül nagy méretű spektroszkópiai adatbázisok kezelésére, ez a MARVEL (Measured Active Rotational-Vibrational Energy Levels; inverz, Hamilton-operátor nélküli megközelítés nagy pontosságú rezgési-forgási energiaszintek meghatározására) eljárás. A MARVEL filozófiája jelentősen eltér a korábban alkalmazott megközelítésekétől. Például ha valaki egy kísérlet során kapott valamilyen eredményt egy molekulára, ezt talán összevetette a hasonló körbe tartozó kísérleti adatokkal, de ennél messzebb nem ment. Tehát a rendelkezésre álló kísérleti információ nagyon kis részét használta fel. Ezzel szemben mi azt javasoljuk – a spektroszkópia kapcsán, de a módszert például a termokémiára is alkalmaztuk –, hogy gyűjtsük össze az összes rendelkezésre álló kísérleti eredményt, és ebből állítsunk elő egy hálózatot úgy, hogy a gráfelmélet és a statisztika által nyújtott segítséggel maximális információt nyerjünk ki az összes elvégzett kísérletből. Ugyancsak javasoltuk, hogy ugyanezt végezzük el a számításokkal is, azaz ne csak kísérleti, hanem elméleti hálózatokat is képezzünk.
 
Hogyan „működik” a rendszer?

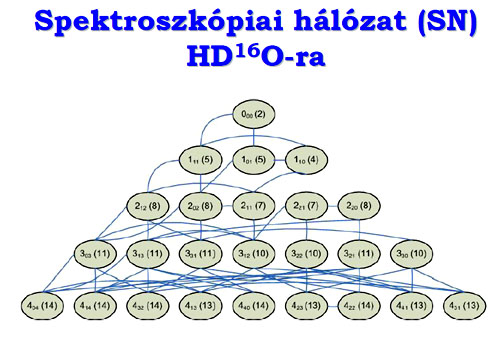
Nézzük a spektroszkópiát. A molekuláknak vannak energiaszintjei, és ezek között létrejöhetnek „ugrások”, a kvantumkémia által diktált kiválasztási szabályok betartásával. Ha az egymás utáni ugrásokkal visszaérek egy körben a kiinduláshoz, akkor a kör meghatározza, hogy az egyedi energiaszintek közötti átmeneteknek, amiket mérek, vissza kell érniük a kiindulási állapothoz. Ezt a gráfelméletben ciklusnak hívják.
 
A gráf csúcsai az energiaszintek, és az élek az átmenetek?

Igen, és vannak olyan energiaszintek, amelyek csomópontként („hub”-ként) viselkednek. Ha a tudásom nagyon pontos a csomópontokra, akkor már pontosan földerítettem a hálózat egyik legfontosabb részét.

A csomópontba sok él fut be. A spektroszkópiában miért viselkednek egyes energiaszintek csomópontként?

A csomópontról sok mérhető átmenet indul. A molekulák rezgőmozgásának megfelelő energiaszintek nagyon messze vannak egymástól, a forgómozgásnak megfelelők pedig nagyon közel. Minden rezgési energiaszintre sok forgási rakódik rá. Egy háromatomos molekulának van kb. ezer rezgési és több százezer rezgési-forgási energiaszintje, és mindre tud „ugrálni” bizonyos kiválasztási szabályokkal. Annál az intenzitásnál, ahonnan ez az ugrás észlelhetővé válik – mert az ugrásokhoz intenzitás köthető a kísérlet révén –, van egy „vágás”.

A kísérlet dönti el, hogy melyik energiaszint viselkedik csomópontként?

Tulajdonképpen igen. Ha különböző jellegű kísérleteket végzek – a spektroszkópiában ez például abszorpciós és emissziós kísérleteket jelent –, akkor különböző csomópontjaim lehetnek.

 

Ez nagyon érdekes!

Igen, mert eddig egész másképp gondolkoztunk. Sok kedvező visszajelzést kaptunk a Furtenbacher Tibor kollégámmal közösen jegyzett cikkeink kapcsán, és szerencsére például Lovász Lászlót, a gráfelmélettel is foglalkozó neves matematikust is érdekelte a spektroszkópiai hálózatok rendszere. Érdeklődő munkatársakat is javasolt nekünk (Faller Beátát és Kaszanitzky Viktóriát), akik segítettek a gráfelméleti feladatok megoldásában.

A matematikusok, fizikusok sokféle mesterséges hálózat vizsgálatával próbálkoznak. A spektroszkópiai hálózat, amit én „természetes” hálózatnak tekintek, hiszen a kvantummechanika, nagy szavakkal a „Természet” hozza létre, ugyanúgy viselkedik, mint a komplex mesterséges hálózatok – akkor, ha vágunk az intenzitásban. Említettem, hogy a mérés csak bizonyos intenzitás fölött képes észlelni az átmenetet. Ezt hívjuk vágásnak. De akárhol vágok, skálafüggetlen hálózat áll elő (1). A skálafüggetlen hálózatok sztochasztikus jelenségek kapcsán lépnek fel, a miénk pedig determinisztikus hálózat, de a vágás véletlenszerű elemet visz bele, és ettől majdnem olyan, mint a skálafüggetlen hálózatok. A spektroszkópiában százmillió elemű adatbázisokkal van dolgunk. Még a vágások után is nagy hálózatok maradnak, sok százezer éllel és sok millió csúccsal.

Az összes olyan tudományos területen (pl. a spektroszkópiában és a termokémiában), ahol adatbázisba rendezték a tudást, ugyanezt a hálózati alapú megközelítést érdemes alkalmazni. Úgy érzem, ez a szemléletmód kiváló lehetőséget nyújt arra, hogy minden egyes új adatot, amit beviszek, a teljes hálózattal szemben ellenőrizhessek. Ha csak kis körben folytatom le az ellenőrzést, sokkal több adat tűnik jónak, mint amikor a teljes hálózatot nézem. Ha tudunk csúcsokat, éleket, esetleg súlyokat definiálni, akkor az adatbázist érdemes hálózatba rendezni, mert minden egyes ciklus adatellenőrzésre nyújt lehetőséget. A spektroszkópia elképesztő mennyiségű ciklust szolgáltat: a spektroszkópiai hálózat többnyire világosan megmutatja, hogy melyik mérés, melyik adat jó és melyik rossz.

Mit tanítanak, vagy mit kellene tanítani kvantumkémiából az egyetemen?

Atkinsnek van egy többkötetes fizikai kémia könyve, és ennek nagyjából a harmada az, amit elméleti kémiának nevezhetünk. Ezt az arányt – a képzésben – az ELTE-n sem éri el az elméleti kémia, máshol pedig még kevésbé. A kémiának nincs más elmélete, mint a kvantummechanika vagy szűkebb értelemben a kvantumkémia. Akkor pedig ezt tanítani kell. Ma már egy szövegszerkesztőt szinte nehezebb használni, mint az elektronszerkezet-számolásra szolgáló modern kvantumkémiai programokat, amelyek „fekete doboz”-szerűen viselkednek. Aki mér, az manapság számol is. Száz atomig lassan már a telefonján is bárki elvégezheti a számolásokat.

SV

---------
1. „A véletlen hálókban – amiatt, hogy a csomópontokat véletlenszerűen kapcsoljuk össze – "demokratikus rendszer" alakul ki, amelyben a legtöbb csomópontba ugyanannyi huzal fut be. Ha például elképzeljük, hogy egy ilyen háló a társadalmat írja le, ahol a csomópontok az egyének és a huzalok az emberek közötti kapcsolatok, akkor egy Erdős-Rényi-féle [“véletlen”] világban megjelenne a demokrácia. A legtöbb embernek nagyjából ugyanannyi barátja lenne, nagyon kevésnek lenne csak sokkal több vagy sokkal kevesebb. A [skálafüggetlen] világhálón ez nem így van: a legtöbb oldalra csak nagyon kevés más oldal mutat, ezek tehát majdnem láthatatlanok a világhálón, néhány oldalra pedig majdnem mindenki rámutat. Azt, hogy hány olyan oldal van, amelyre majdnem senki sem mutat, és hányra mutatnak rengetegen, hatványfüggvénnyel írhatjuk le.” (Beszélgetés Barabási Albert-Lászlóval, Természet Világa, 2005. február.)