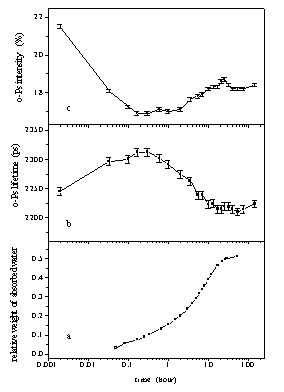
Figure 1. Swelling kinetics of the PDMAEMA-l-PIB amphiphilic
network
followed gravimetrically (a) and by positron lifetime spectroscopy
(b,c).
Orto-pozitróniumatomok kölcsönhatása szerkezeti szabad térfogatokkal
Eötvös Loránd Tudományegyetem, Budapest
1999
Bevezetés és célkitûzés
Kondenzált fázisú nem kristályos anyagok egyik fontos szerkezeti jellemzõje az anyag atomjai és molekulái között levõ kis elektronsûrûségû helyek - szerkezeti szabad térfogat - szerkezete és mérete. Az orto-pozitróniumatomok (o-Ps) annihilációs paraméterei értékes és egyedi információkat szolgáltatnak a szerkezeti szabad térfogatról. Az o-Ps atomok ezen tulajdonságát szemlélteti ezen munka is egy gyakorlati és egy elméleti példán keresztül.
Az amfifil kotérhálók olyan különleges fizikai és kémiai tulajdonságokkal bíró anyagok, amelyek kovalens kötésekkel összekapcsolt hidrofil és hidrofób láncokat tartalmaznak. Különleges duzzadási (poláros és apoláros oldószerekben is jól duzzadnak) és szövetbarát tulajdonságaik miatt rendkívül ígéretes anyagok lehetnek az orvosi gyakorlatban, mint szövetpótló implantátumok, vagy gyógyszerhordozó mátrixok. Az ilyen típusú térhálókat csak a 90’-es években sikerült elõállítani, ezért szerkezetük és tulajdonságaik vizsgálata a kezdeti szakaszban tart. Az amfifil kotérhálók duzzadását csak “hagyományos”, tömegmérésen alapuló módszerrel vizsgálták, pozitronélettartam mérések alkalmazása újdonság ezen a területen. A duzzadás mechanizmusának és dinamikájának felderítése céljából különbözõ oldatszerkezeti vizsgálatokat (pozitronélettartam-, FTIR méréseket illetve ab initio számításokat) végeztem. A vizsgálatok összegzése és értelmezése lehetõséget nyújt az amfifil kotérhálók szisztematikus tanulmányozásának megalapozására.
A szabad térfogat modell (“free volume model”) kidolgozói
egyszerû, néhány mérési eredmény
felhasználásával készített egyenletet
dolgoztak ki, amely lehetõvé teszi a mért o-Ps élettartamból
a szabad térfogat méretének kiszámítását.
Az egyenletet ma már széles körben használják,
elsõsorban polimerekben levõ szabad térfogat méretének
és méreteloszlásának számolására.
A modell olyan egyszerûsítõ feltételeket is
tartalmaz, amelyek miatt a kapott eredmények és következtetések
megkérdõjelezhetõek. A szabad térfogat modell,
amely néhány viszonylag régi, a mai lehetõségeknél
pontatlanabb mérésen alapul, legfõbb hibája
az, hogy nem veszi figyelembe a kémiai környezet hatását
az o-Ps atom élettartamára. Ez a hiányosság
azonban pótolható a perturbációszámításon
segítségével.
Vizsgálati módszerek és eredmények
A pozitronélettartam mérésekhez gyors-gyors koincidenciakört
(ORTEC) használtam. A detektorokban Philips 2020Q fotoelektron-sokszorozó
és BaF2 szcintillátorkristályok voltak.
A többcsatornás analizátorkártya minden mérésnél
5·106 eseményt regisztrált, a berendezés
felbontása 210 ps volt. A mért spektrumokat a RESOLUTION
programmal értékeltem ki. Az FTIR (Fourier transzformált
infravörös spektroszkópia) méréseket egy
Bruker IFS55 spektrométerrel végeztem, amelyben trapezoid
(45° ) KRS55 kristály volt. A spektrumok felvételénél
ATR (totál reflexiós) technikát használtam.
Az ab initio számításokat a GAUSSIAN '94 program
felhasználásával végeztem. A poli[2-dimetilamino(etil-metakrilát)]-l-poliizobutilén
(PDMAEMA-l-PIB) amfifil kotérháló 48% hidrofób
(PIB) és 52 % hidrofil (PDMAEMA) láncot tartalmazott.
Az amfifil kotérháló duzzadása
A pozitróniumatomok annihilációs paraméterei jelentõs változást mutattak a duzzadási folyamat során. Jól megfigyelhetõ például a vízfelvétel telítése, az orto-pozitrónium élettartama és képzõdésének valószínûsége kb. 50 óra után éri el az egyensúlyi értéket. A duzzadás kezdeti szakaszában az orto-pozitrónium élettartama nõ, amit a térhálóban levõ szabad térfogat méretének növekedése okoz. A folyamat elõrehaladtával a polimermolekulák közti szabad térfogatokat kitöltik a vízmolekulák, így az élettartam a tiszta vízben mérhetõ érték irányába tolódik el. A pozitróniumképzõdés valószínûsége a duzzadási folyamat elején csökken, amit nem indokol a szabad térfogat méretének növekedése. A nem várt jelenség magyarázata a hidrofil lánc és a vízmolekulák között kialakuló másodrendû kötések kialakulásában, azaz az elektronszerkezet változásában rejlik.
A duzzadás mechanizmusa és a folyamat közben bekövetkezõ elektronszerkezeti változások megismerése céljából a hidrofil lánc monomerjének (2-dimetilamino(etil-metakrilát) - DMAEMA) vizes elegyeit vizsgáltuk. A pozitronélettartam mérések eredményeibõl megállapítható, hogy a duzzadás kezdeti szakaszában bekövetkezõ élettartamnövekedésért a szabad térfogatok átlagos méretének növekedése, a képzõdési valószínûség csökkenéséért a monomermolekulák és a vízmolekulák között kialakuló hidrogénhidas kötések felelõsek. Az otro-pozitrónium képzõdési valószínûsége az 1:1 mólarány eléréséig csökken (további víz hozzáadása nem befolyásolja), ami azt mutatja, hogy az 1:1 molekulaarányú "klasztereknek" kitüntetett szerepe van.
A másodrendû kötések által stabilizált monomer-víz “klaszterek” szerkezetének felderítése céljából FTIR-spektroszkópiai méréseket és ab initio számításokat végeztünk. Az FTIR mérések azt mutatták, hogy már nagyon kicsi vízkoncentrációnál is hidrogénkötések alakulnak ki a monomermolekulák amino- és karbonilcsoportjai, valamint a vízmolekulák között. Erre a két funkciós csoport rezgési sávjának eltolódásából, és a vízmolekulák O-H sávjának struktúráltságából következtettünk.
Az ab initio számítások eredményei azt mutatták, hogy a vízmolekulák közel azonos energiával kötõdnek mind a karbonil-, mind az aminocsoporthoz. Abban az esetben, ha intramolekuláris gyûrû alakul ki (az amino- és a karbonilcsoport ugyanazzal a vízmolekulával alakít ki hidrogénhíd kötést), a rendszer energiája jelentõsen csökken. Az energiakülönbség az alkalmazott bázistól függõen 20-40 kJ/mol, ami elegendõ lehet ahhoz, hogy az intramolekuláris “klasztert” energetikailag kitüntesse.
A különbözõ vizsgálatok eredményeinek
összegzésével az amfifil kotérháló
vízben történõ duzzadásának mechanizmusa
és dinamikája a következõképpen foglalható
össze. A duzzadási folyamat elején kis mennyiségû
víz hatására a hidrofil láncok kitágulnak,
ezzel párhuzamosan a hidrofób láncok összehúzódnak,
aminek eredményeként a polimermolekulák közti
szabad térfogatok átlagos mérete megnõ. A hidrofil
láncok az üregek belseje felé fordulnak, a monomermolekulák
a vízmolekulákkal intramolekuláris gyûrût
alkotnak. A folyamat gyors (kb. 10 perc), ezért valószínû,
hogy a megnövekedett méretû szabad térfogatot
alkotó üregeket csatornák kötik össze, illetve
a szabad térfogat csatornás szerkezetû. A megváltozott
szerkezetû térháló nagy mennyiségû
vizet képes felvenni, a telítést kb. 50 óra
alatt éri el.
Perturbációszámítás az o-Ps atomon
Az általam kidolgozott modellben a pozitróniumatomot gömbszimmetrikus, periodikus potenciáltérbe helyeztem. A potenciál periodicitása a rácsállandót, magassága a kémiai környezetet jellemzi. Megoldottam az alapállapotú pozitróniumatom Schrödinger-egyenletét a nemdegenerált Rayleigh-Schrödinger perturbációs elmélet felhasználásával. A sajátfüggvények és a Bloch-tételnek megfelelõen választott elektronsûrûség átfedésének segítségével kiszámítottam a pozitróniumatom perturbált élettartamát.
Számításaim szerint a pozitróniumatom energiáját jelentõsen befolyásolja a kémiai környezet és a periodicitás is. Nagy perturbáció esetén (kis rácsállandó, nagy elektronsûrûség) az energia pozitívnak adódik, azaz nem képzõdhetnek pozitróniumatomok. Ez a kísérleti tapasztalatokkal jó egyezést mutat, hiszen fémekben nem képzõdik pozitrónium.
Perturbáció hatására a pozitróniumatomok gerjesztõdnek, ennek megfelelõen a sajátfüggvényekbõl számolható sajátannihilációs élettartamok növekednek. Nagyobb perturbáció azonban nagyobb elektronsûrûséget jelent, ami gyorsítja a “pick-off” folyamatok sebességét, ami az élettartam csökkenését okozza. A két annihilációs folyamat összegzéseként kiszámítottam az orto-pozitróniumatomok teljes élettartamát. Eredményeim - a várakozásoknak megfelelõen - azt mutatták, hogy az élettartamot nemcsak a szabad térfogat mérete, hanem a kémiai környezet is jelentõsen befolyásolja. Számításaim eredményei alapján a szabad térfogat modell eredeti formájában inkább csak azonos kémiai összetétel esetén a szabad térfogat méretének, és méretváltozása irányának becslésére alkalmas.
Interaction of ortho-positronium with free volume
Ph.D. Thesis, Eötvös Loránd University
Budapest
1999
Introduction
Positron lifetime technique has been extensively used to study the structure of polymers recently because it provides a unique possibility to investigate the free volume through the lifetime of ortho-positronium atoms (o-Ps). This property of positronium atoms is demonstrated by an experimental and a theoretical example.
As recent investigations with polyisobutylene(PIB)-based amphiphilic conetworks (APCNs) indicate, the covalently bonded immiscible hydrophilic and hydrophobic segments result in unique nano-structured molecular composites with co-continuous microphase separated morphology. Most likely this special structure explains the excellent biocompatibilty and blood compatibility of these materials. These polymeric materials are swellable both in hydrophilic and hydrophobic solvents, and the equilibrium swelling is controlled by composition. One of unique aspects of the swelling process of APCNs is that the polymer phase with opposite philicity of the solvent is expected to collapse or shrink during swelling. The o-Ps is localised in the free volumes between the polymer chains and its annihilation takes place by external electrons.
Several authors published correlation functions between the lifetime
of o-Ps and the size of free volume units in molecular systems but these
correlations are valid only for uniform chemical compositions. The most
widely used model for calculating positronium lifetime in condensed materials
applies a variant of the particle-in-a-box approximation. It replaces the
actual Bloch-potential with a periodic rectangular potential and places
o-Ps in a rectangular potential well of semi-infinite depth. The most serious
simplification of this model is the assumption that the density |yPs|2
is zero at the boundaries of the potential well. This simplification leads
to the greatest advantage of this model, i.e., it provides a simple equation
establishing connection between o-Ps lifetime and free volume. On the other
hand, recent experiments and theoretical considerations revealed some disadvantages:
the potential well is always spherical, o-Ps is localized totally and the
electron density is always the same independently of the chemical composition
and the crystal structure. In this work we performed calculations on a
somewhat more realistic model using perturbation theory.
Swelling dynamics and free volume structure of amphiphilic conetwork (APCN)
Experimental
For positron lifetime measurements we applied a fast-fast coincidence system having a time resolution (FWHM of the resolution curve) of about 200 ps. The spectra were decomposed into three lifetime components by the help of the RESOLUTION computer code. The FTIR spectra were recorded on a Bruker IFS55 spectrometer using the ATR technique with trapezoidal (45o) KRS5 crystal.
Results and discussion
As the conventional swelling ratio measurements shows (Fig. 1a), the investigated DMAEMA-l-PIB is able to absorb large amount of water. The water uptake is relatively quick at the beginning but saturation (equilibrium) occurs only after ~50 hours soaking at 52 % swelling ratio at room temperature. Significant changes occur in the lifetime and the intensity of o-Ps as a function of swelling time (Fig. 1b and Fig. 1c). At the beginning of the swelling process, i.e. at low swelling ratios, the o-Ps lifetime increases by about 70 picoseconds, then it reaches a maximum and decreases again. In this latter phase, the decrease of the lifetime is the expected phenomenon, and it is related to the filling of the free volume by water. As the water molecules fill the free volumes in the network by reaching equilibrium swelling, the o-Ps lifetime approaches the value measured in pure water (about 1800 ps).

Figure 1. Swelling kinetics of the PDMAEMA-l-PIB amphiphilic
network
followed gravimetrically (a) and by positron lifetime spectroscopy
(b,c).
The increase of the lifetime at very low swelling ratios indicates that the average size of free volume sites increases in the PDMAEMA-l-PIB network as water molecules start to diffuse in the material. Surprisingly, these dynamic structural changes occur fast at the very beginning of the swelling process and at low swelling ratios. Considering the amphiphilic nature of the PDMAEMA-l-PIB sample, this observation can be explained by a quick rearrangement of the phases with opposite philicity in this APCN. The PDMAEMA phase expands whereas the PIB phase shrinks upon contacting with water. Both effects yield an increase of the size of free volume units.
The o-Ps formation intensity rapidly decreases at the beginning of the swelling process and after reaching a minimum it increases again (Fig. 1c). The interpretation of the decrease of the o-Ps formation intensity is not as straightforward as that of the lifetime changes. It cannot be explained either by the free volume increase or by the direct effects of water, i. e. the increase of free volume size does not have a significant effect on Ps formation and the Ps formation intensity is higher in pure water than in the network.
Lifetime measurements were also performed in water/DMAEMA mixtures in order to study the intensity decrease. The results show (Fig. 2) that an intensity decrease occurs when adding water into the DMAEMA monomer similar to that observed as in the APCN. In the solution the o-Ps formation intensity decreases till the water/DMAEMA molar ratio reaches one and further addition of water does not affect this parameter significantly. These results suggest that the "adsorption" of the first water molecule to the coordination sphere changes the electronic structure of DMAEMA molecules, so that it provides smaller probability for o-Ps formation. On the basis of our results we concluded that 1:1 DMAEMA/water clusters were formed in the sample.
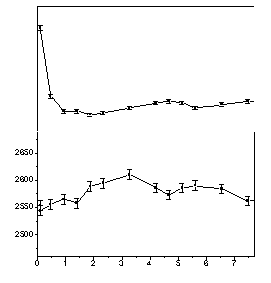
Figure 2. Positron lifetime parameters in the mixtures of the DMAEMA monomer and deionized water.
The most obvious way to explain the formation of 1:1 clusters is the assumption that one of the possible groups of DMAEMA forms a more stable H-bond with water. Unfortunately, the FTIR results disproved this assumption showing that both groups (carbonyl and amino) form hydrogen bond at the smallest investigated water concentration. The characteristic vibrations of both C-N and C=O groups shifted significantly (15 cm-1) as the molar ratio of water increased in DMAEMA. This result shows clearly that both groups form hydrogen bond even at very low water concentrations.
For the exceptional explanation of the role of 1:1 molar ratio quantum
chemical ab initio calculations were performed for the DMAEMA monomer.
It was supposed that H-bonded clusters were formed in the mixtures and
1:1 clusters are the most stable among them. In order to confirm this assumption
optimum geometries and total energies were calculated for 1:1 clusters
of different structures. The calculated total energy difference between
N--H-O and O--H-O clusters is very small (Table 1).
Table 1. The total energies for different 1:1 DMAEMA/water clusters
obtained by different ab initio methods.
All data refer to the optimum geometry of the given calculation level.
|
|
|||||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
# The optimum geometry was not found although several initial configurations were tested.
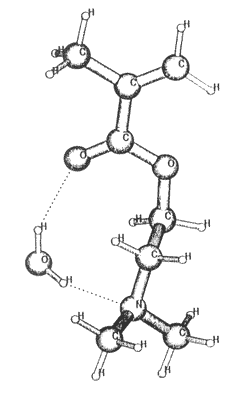
Figure 3. The structure of the DMAEMA:water hydrogen bonded cluster.
The figure represents the optimized geometry calculated by DFT(B3LYP)/6-31G**
(see also Table 1).
There are two other possible cluster structures which distinguish the 1:1 ratio of water and DMAEMA. The first is a chain-like structure in which DMAEMA and water molecules are ordered alternately connected to each other by H-bonds. As we suppose that same phenomenon responsible for the APCN, the exceptionality of 1:1 clusters in both DMAEMA and the APCN, the chainlike structure can be excluded. This is a very unlikely structure in APCN. A little more reliable explanation is provided by the assumption of "intramolecular" H-bonded ring formation (Fig 3.). The calculated energy gain of this cluster is might be enough for the formation of the N--HOH--O structure. It should be noted that the formed clusters do not necessarily live forever but their lifetime is long enough to affect positronium formation intensity.
Since the o-Ps formation intensity data of the PDMAEMA-l-PIB APCN are very similar to those of the water/DMAEMA mixtures, we can assume that the hydration of the APCN occurs in a similar way, i.e. the formation of ring-like 1:1 clusters is also the first process in the network. This assumption is confirmed by the fact that the intensity decrease continues in the network till the water/DMAEMA mole ratio reaches the unit value (in about 8-10 minutes). The fact that the intensity decrease stops at this mole ratio suggests that water molecules are able to reach every DMAEMA unit very quickly at the beginning of the swelling process. If the free volume were composed of independent pores the intensity decrease would be a slow process and would not stop at 1:1 water/DMAEMA ratio. On the other hand the observed changes indicate that the surface of the free volume units become covered with water molecules quickly at the beginning of swelling. This suggests that the free volume in the PDMAEMA-l-PIB APCN is composed of interconnected channels which allow rapid diffusion of water molecu-le to cover the surface of the free volume units in this APCN.
Results of this study also indicate that positron annihilation can be
successfully applied not only for obtaining information on free volume
changes in polymeric materials but also on the dynamics of swelling and
the structure of free volume in certain macromolecular systems, such as
networks, hydrogels, polyelectrolyte gels, polymer composites, blends,
etc., by studying the swelling kinetics and positron lifetime parameters
simultaneously. We think that the results of this study can be extended
for the investigation of a wide variety of gels and amorphous materials
as well.
Perturbation theory calculations on o-Ps atom
Theory and mathematical method
In our calculation, as a starting point, we chose one dimensional potentials (Ps in spherical void) for which the non-relativistic, non-degenerate Rayleigh-Schrödinger pertur-bation theory applies. This theory replaces the ground state Schrödinger equation H0y0=E0y0 with a somewhat different equation Hy =(H0+V)y =Ey in which V is the perturbation potential. The perturbed wave function and its energy are given by the following equations:
y = y0
+ y 1+ y2
+ ... , 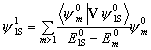 ,
,
where the upper indexes indicate the order of perturbation and m runs over all the unperturbed wave functions. In our calcul-ations we chose m=2S, 3S,..., 20S and stopped after first order perturbation.
For the classic one dimensional Bloch- perturbation potential we chose the potential:
![]()
Results and discussion
The results of the calculations show that the shape of the perturbed wave function depends on the periodicity of the potential very much. Below a=4 a.u. the consecutive electron density minima follows each other very densely, which does not give any possibility for the formation of partially populated 2S, 3S, etc. shells. Instead, the perturbed wave function resembles the 1S-state very well (Fig. 4a) although the average size of o-Ps increases a little. On the other hand, at larger values of a the partially populated S-states occur quite clearly in the perturbed wave function (Fig. 4b).
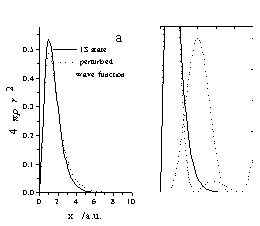
Figure 4. Perturbed wave functions produced by different perturbation
potentials.
The periodicity was chosen as a=3 a.u. for a) and a=8 a.u. for b) and
the amplitude q=0.25 for both cases.
The most important consequence of Figure 4 is that the positronium density |YPs|2 is non-zero at the boundaries of the potential well. In other words the positronium is not localized totally in the potential well. This is independent of the periodicity, the amplitude, and the shape of the potential: the probability of finding the positronium outside the well is always larger than zero. Consequently, treating positronium as a particle in a box seems to over-simplify models for calculations.
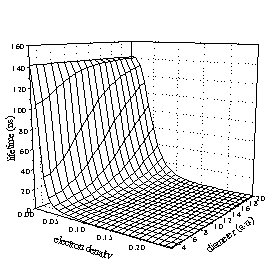
Figure 5. Dependence of the lifetime of o-Ps on the period-icity
(a)
and the amplitude (q) of the perturbation potential.
From the perturbed wave function the lifetime of self-annihilation can be calculated as it is calculated for ground state positronium in a vacuum. The problem is raised by the pick-of annihilation because the electron density of the material is usually unknown. To avoid this problem we applied a classic method and calculated electron density which is proportional to the square of the potential. This electron density depends on q and a and simulates the chemical and crystallographic properties of materials. According to this electron density we calculated the lifetime and the binding energy of o-Ps for a wide range of potentials.
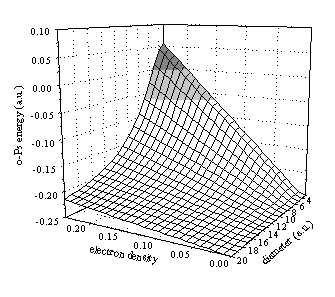
Figure 6. Dependence of the o-Ps energy of o-Ps on the periodicity (a) and the amplitude (q) of the perturbation potential. The darker shading indicates positive binding energies and the lighter indicates energies of higher S-states.
The calculated lifetime surface is given in Figure 5 indicating a strong dependency of the lifetime on electron density. However the rapid lifetime changes occur at small perturbations and in the nanosecond range (where lifetime measurements are usually performed) the surface is almost plain. This means that former calculations did not necessarily provide erroneous results assuming the electron density to be constant for a wide selection of materials. Our calculations revealed that in the nanosecond range the lifetime depends much more strongly on periodicity than on "chemical surroundings".
We considered the roles of self-annihilation and pick-off in the formation of the lifetime of o-Ps. It turned out that below 100 ns the lifetime is determined almost exclusively by the pick-off process. The role of self-annihilation is less than the experimental error of measurements.
The energy surface (Fig. 6) provides a test to decide on the reliability
of the calculations. As it is shown by the figure, the model provides the
expected results. The positronium becomes less and less stable as we increase
the electron density (q) and as we decrease the size of the potential well
(a). The calculation gave positive binding energies (i.e. no positronium
formation) for materials with large perturbation potential and small periodicity
(e.g. metals).
References
1. A. Domján, B. Iván, K. Süvegh and A. Vértes,
J. Radioanal. Nucl.Chem. Articles 211(1), (1996) 219
2. K. Süvegh, A. Domján and A. Vértes, J. Radioanal.
Nucl. Chem. Articles 211(1), (1996) 203
3. K. Süvegh, A. Domján, G. Magyarfalvi, Gy. Vankó
and A. Vértes, Mat. Sci. Forum 255-257, (1997) 348
4. A. Domján, K. Süvegh and A. Vértes, Mat. Sci.
Forum 255-257, (1997) 251
5. B. Iván, K. Süvegh, A. Domján, Gy. Vankó
and A. Vértes, Macromolecules 31, (1998) 770
6. A. Domján, B. Iván, K. Süvegh, Gy. Vankó,
A. Vértes, Polym. Mater. Sci. Eng. 79, (1998) 455
7. A. Vértes, K. Süvegh, M. Bokor, A. Domján, T.
Marek, M. Klapper, C. U. Chisholm, M. El-Sharif, K. Tompa, J. Radioanal.
Nucl. Chem. Articles 239, (1999) 29
| Vissza a tartalomjegyzékhez
Back to Contents |
http://www.kfki.hu/chemonet/
http://www.ch.bme.hu/chemonet/ |