
Ahelyett, hogy a tanárnak kellene megmondani, mit kell tudni a tengelyekrôl és a koordinátarendszerekrôl, a fraktálok hatására a diákok fordulnak hozzá az ezekre vonatkozó kérdéseikkel. Erre a fraktálok vizsgálata közbeni "kalandok" inspirálják a diákokat. Sok diák szeretné elmondani a barátainak, hogy hol találhatnak érdekes részeket a Mandelbrot-halmazon belül - és természetesen az is elôfordul, hogy saját maguk számára szeretnének megjegyezni egy-egy helyet. Ezek miatt az igények miatt fordulnak a tanárhoz. Ha megtudják, hogy egy-egy területet két szám és egy nagyítás segítségével meg lehet határozni, akkor hamarosan megindul az osztályban a koordináták cseréje. A diákokat az is megigézi, mikor megtudják, hogy ezeket a pontokat nemcsak két számmal, hanem egy számmal és egy szöggel is meg lehet adni. így a polárkoordináta-rendszer nem lesz a számukra egy elvont fogalom, hiszen fel tudják használni valamire. Az általános iskolában még nem szükséges, hogy bonyolítsuk a képet azzal, hogy megmondjuk a diákoknak, hogy a szóban forgó rendszer a komplex síkon helyezkedik el. Talán a legfontosabb eredmény az, hogy a diákok megtanulják, hogyan lehet a tengelyek segítségével helyeket kijelölni.
Két másik területet is megismerhetnek ezen a ponton a diákok. Egyrészt igen hamar felismerik, hogy egyes számok negatívak, míg mások pozitívak. Tudni akarják, hogy ez miért van így - így már el is jutottak a tengelyek pozitív és negatív felének a megismeréséig. Másrészt a diákok megismerik a helyiértékek fogalmát is, mert kalandozásaik során szükségük lesz ezek megfelelô használatára. Ennek oka az, hogy a számítógépek - a programozásukból kifolyólag - az egynél kisebb, ill. a tíznél nagyobb számokat a tudományos szisztéma szerint jelölik. így pl. a 0.071563 helyett a gép 7.1583e-2-t ír ki. Ha a diákok nem veszik figyelembe az exponenst, akkor téves információkat fognak átadni egymásnak - és elôbb-utóbb kíváncsiak lesznek ennek az okára.
A diákok élvezik a Mandelbrot-halmaz nagyítgatását - és ezt az élvezetet a tanár könnyedén felhasználhatja arra, hogy megismertesse velük az összeadást és a kivonást. ha az eredeti halmazt úgy tekintjük, mintha egy testbôl (a vese alakú rész), fejbôl (a test utáni legnagyobb dudor), két karból (a fej utáni legnagyobb dudorok) és több, egyre kisebb dudorból állna, akkor könnyen fedezhetünk fel szabályszerûségeket a dudorok periódusa) és a helye között. A periódus azon pozíciók számával egyenlô, amelyeket a kiválasztott pont végtelen számú iteráció során elfoglal. Például a fôtestben levô pontok bármelyikének a periódusa egy lesz (1/a. ábra)
 |
1/a. ábra: A "test" belsejében kiválasztott pontokhoz különbözô pálya és periódus tartozik. |
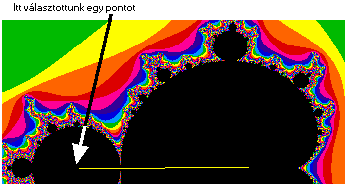 |
1/b. ábra: Egy pont a "fejbôl". |
 |
1/c. ábra: A "fej" hármas periódusú. |
A fejben kiválasztott tetszôleges pont két végpont között mozog, míg a két kar periódusa három - mint ez az 1/b. és 1/c. ábrákon látható. Ha megvizsgáljuk a testbôl kinövô, a fej és a kar között elhelyezkedô legnagyobb dudort, annak a periódusára öt adódik (1/d. ábra).
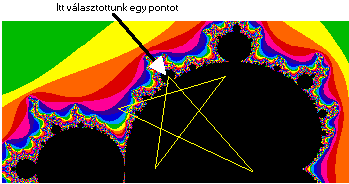 |
1/d ábra: Egy ötös periódusú dudor. |
A hármas és az ötös periódusú dudor közti legnagyobb gumó nyolcas periódusú lesz (1/e. ábra). ez az összeadásos séma tetszôlegesen folytatható, mindaddig, amíg a fôtestbôl kinövô, két , az elôzôleg legnagyobb gumó közti legnagyobb dudorról van szó.
 |
1/e. ábra.: Egy nyolcas periódusú dudor, ami a hármas és az ötös közti legnagyobb. |
A szorzás akkor kap szerepet, ha elhagyjuk a fôtestet és más dudorokat kezdünk el vizsgálni. Ha egy, az elôzôekben ötösként megállapított periódusú dudort kinagyítunk, akkor tekinthetô ez a dudor is egy új "fô test"-nek, amihez ugyanúgy tartozik fej és két kar, valamint több kisebb dudor. Ez az új test hasonló (illetve majdnem hasonló) lesz az eredetihez. Kiderül, hogy ebben a testben a kar pontjainak periódusa 15, ami nem más, mint a szorzata az ötnek (az új fôtestként kiválasztott dudor eredeti periódusának) és a háromnak (ami a kar relatív periódusa). Emlékezzünk arra, hogy a testek relatív periódusa egy, a fejeké kettô, a karoké három, a következô legnagyobb dudoroké öt, és így tovább (mindig összeadva a dudort közrefogó két nagyobb dudor periódusát). Például, ha megvizsgáljuk a kezdeti halmaz (hármas periódusú) karjában levô karok periodicitását, eredményül kilencet kapunk. Ezt könnyû kiszámolni, hiszen a kar csupán egy hárommal való szorzást jelent, és mi épp egy kar karját vizsgáltuk. Hasonlóképp, ha ennek a karnak a fejét vizsgáljuk, akkor a periódus hat lesz, mivel a karok hármas szorzónak, a fejek pedig kettes szorzónak felelnek meg, és csak egy szintet mentünk le.
Most, hogy már tudjuk, hogy az összeadás segítségével kiszámolhatjuk a két dudor közti dudor periódusát, míg szorzással a dudoron-dudor esetet vizsgálhatjuk meg, megismerkedhetünk a disztributivitás szerepével is. Például nézzük csak meg az eredeti halmazban a kar és a fej közti legnagyobb dudort! Mivel a fej periódusa kettô, míg a karé három, tudjuk, hogy ezé öt lesz. Ha ennek a dudornak a fejét vizsgáljuk, akkor - mint már tudjuk - a periódusa tíz lesz, mivel a fej relatív periódusa (kettô) megszorzódik a testet képzô dudor abszolút periódusával (ami öt), azaz 5*2=10. Ugyanígy, ennek a dudornak a karja 15-ös periódusú lesz, mivel 5*3-15. Tehát mekkora is a periódusa egy ötös periódusú dudornál a dudor feje és karja közti legnagyobb dudornak (2. ábra)?
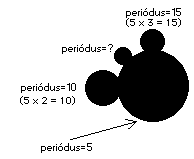
2. ábra: Egy ötös periódusú dudor néhány aldudorral.
Akárcsak az eredeti Mandelbrot-halmaznál, tekinthetjük ezt a dudort a testnek, a belôle kinövô legnagyobb dudort a fejnek, az az utáni legnagyobbakat a karnak, stb. A fej periódusa mindíg a test periódusának a kétszerese, a kar periódusa pedig a test periódusának a háromszorosa. Ezeknek a tudatában két különbözô úton is megállapítható a kérdéses dudor periódusa.
Elôször is, összeadhatjuk a 10-et és a 15-öt, mivel egy 10-es és egy 15-ös periódusú dudor közti legnagyobb dudorról van szó. Ezt úgy is felírhatjuk, hogy (5*2)+(5*3), mivel eredetileg az ötös periódusú dudortól indultunk el. A másik módszer szerint szorozzuk meg az ötöt öttel, hiszen egy ötös periódusú dudoron lévô ötös periódusú dudort vizsgálunk. Ezt úgy is írhatjuk, hogy 5*(2+3), mivel ez egy ötös periódusú dudoron a (kettes relatív periódusú) fej és a )hármas relatív periódusú) kar közti legnagyobb dudor. Így a Mandelbrot-halmazon keresztül a diákok megtanulhatják, hogy (5*2)+(5*3)=5*(2+3) - és ez a tanulási módszer érdekesebb nekik, mint a számukra jelentés nélküli absztrakt szimulációkkal való bajlódás.
Copyrights 1993, University of Illinois Board of Trustees
National Center for Supercomputing Applications, Education Group
rpanoff@ncsa.uiuc.edu és jgasaway@ncsa.uiuc.edu