Míg a klasszikus geometria egész dimenziókkal foglalkozik, addig a fraktálgeometria nem-egész dimenziókat ír le. A világot eddig úgy ismertük, mint ami nulldimenziós pontokból, egydimenziós egyenesekbôl és görbékbôl, kétdimenziós síkidomokból mint pl. négyzetekbôl és körökbôl, illetve háromdimenziós testekbôl mint pl. kockákból és gömbökbôl áll.
Pedig sok természeti jelenség jobban leírható nem egész számú dimenzióval. Így míg egy egyenes dimenziója egy, addig egy fraktálgörbe dimenziója egy és kettô között van attól függôen, hogy tekeredés és csavarodás közben mekkora teret foglal el (Peterson, 1984). Minél jobban kitölti a síkbeli fraktál a síkot, dimenziója annál jobban megközelíti a kettôt. Hasonlóképpen egy "dombos fraktáltáj" dimenziója valahol kettô és három között van. Tehát egy olyan fraktáltájnak, amely egy nagy dombot tartalmaz kis "hoporcsokkal", kettôhöz közeli lesz a dimenziója, míg egy egyenetlen felületûé sok közepes méretû dombbal már majdnem három (Peterson, 1984).
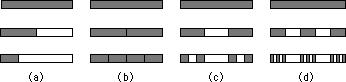
A magyarázathoz elôször definiáljunk egy fraktált az Nn=C/rnD egyenlettel, ahol Nn azon szakaszok száma, amelyek hossza rn, C konstans és D a fraktáldimenzió (Turcotte, 1992). Az egyenletet átrendezés után a D=[ln(Nn+1/Nn)]/ln(rn/rn+1)] alakot veszi fel. Ezek után vegyünk egy egységnyi hosszúságú szakaszt (1. ábra) és osszuk fel. Az 1/a ábrán a szakaszt két részre osztottuk (így r1=1/2), majd az egyik felet megtartjuk, a másikat pedig eldobjuk (azaz N1=1). Ha a megmaradó részt szintén megfelezzük és csak az egyik részét tartjuk meg, akkor r2=1/4, N2=1. Ez esetben D értékeként nullát kapunk - azaz az euklideszi pontot kaptuk vissza. Mindegy, hány lépésig folytatjuk a felosztást, az n-edik lépés után Nn mindenképp 1 lesz, azaz D mindig nulla. Ez könnyen megérthetô, hiszen ahogy folytatjuk ezt a darabolást, a megmaradó rész hossza mindinkább tart a nullához.

1. ábra: Az egységnyi hosszú szakasz darabkáinak fraktáldimenziói
Az euklideszi vonalat ugyanilyen könnyedén visszakaphatjuk (1/b ábra). Ekkor a szakaszt két részre osztjuk, de mindkét részt megtartjuk, így r1=1/2 és N1=2, A következô lépésben r2=1/4 és N2=4. Ezért D=ln(2)/ln(2)=1. Ez is könnyen érthetô, hisz a szakasz mindig egységnyi hosszú marad.
Azonban ugyanilyen egyszerûen lehet egy nulla és egy közti fraktáldimenziójú halmazt készíteni. Mint az 1/c. ábrán látható, felosztottuk a szakaszt 3 részre és a két szélsô darabot tartottuk meg, így r1=1/3 és N1=2. Ha ezt megismételjük, akkor r2=1/9 és N2=4. Így D=ln(2)/ln(3)=0.6309. Ha az egységszakaszt öt részre osztjuk (1/d. ábra), akkor r1=1/5. Ha a két szélsô és a középsô darabot tartjuk meg, akkor N1=3. A következô lépésben r2=1/25 és N2=9. Így D=ln(3)/ln(5)=0.6826. Természetesen a két utóbbi példánál - ha végtelenszer ismételjük meg a felosztást - akkor végül az egyre rövidülô darabokból pontok lesznek. A pontoknak ezt a végtelen halmazát "por"-nak ("dust") nevezik (Turcotte, 1992). Bármilyen nulla és egy közötti fraktáldimenziójú halmazt létre lehet hozni ezzel a módszerrel.
Ugyanúgy, ahogy létrehozhattunk nulla és egy közötti dimenziójú halmazokat, négyzetekbôl kiindulva nulla és kettô köztieket is csinálhatunk. A 2. ábra segít ennek a megértésében (Turcotte, 1992). A képen látható példákban az egységnégyzetet kilenc egyenlô részre osztjuk, ekkor r1=1/3. A következô lépésben ezek a kisebb darabok lesznek ugyanígy kilenc egyenlô részre osztva, így r2=1/9. Mint ahogy a szakasznál is tettük, ezt a felosztást n-szer megismételjük. A 2/a. ábrán mindig csak egy darabkát tartottunk meg, így N1=Nn=1. Ezért D=0 lesz, azaz megint az euklideszi ponthoz jutottunk. A 2/b. ábrán két darabot tartottunk meg az elsô lépésben, így négy maradt a másodikban, és így tovább, azaz N1=2, N2=4, stb. Ezért D=ln(2)/ln(3). Ekkor ugyanazt a dimenziót kaptuk vissza, amit az 1/c. ábránál is kaptunk. Ha három darabot tartunk meg, akkor az euklideszi vonalhoz jutunk (2/c. ábra), mivel N1=3, N2=9. Ha csak mindig a középsô darabot távolítjuk el - azaz N1=8, N2=64 - (ahogy ez a 2/d ábrán látható), akkor a dimenzió 1.8928 lesz. És végül, természetesen ha mindig minden darabot megtartunk (2/e. ábra), akkor a dimenzió 2 lesz, azaz az euklideszi síkhoz jutottunk el. Ugyanígy létrehozhatunk nulla és három közti dimenziókat is, ha egy kockából indulunk ki.
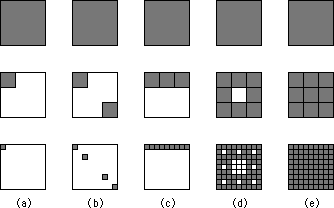
2. ábra: Fraktáldimenziók, egységnyi területû síkidomokból kiindulva
Egy másik módszer a fraktálok készítésére az, hogy a kezdeti szakaszhoz mindig hozzáadunk egy másik szakaszt, ahelyett, hogy darabolnánk. A Koch-görbe - nevét Helge von Kochról kapta, aki 1904-ben elsôként mutatta be ezt az alakzatot - a fraktálok egy jellegzetes példájává vált. Szerkesztése igen egyszerû (Jürgens et al., 1992). Szintén egy egységszakaszból indulunk ki (3/a. ábra), amit három egyenlô részre osztunk. Ezután a középsô szakasz helyére egy egyenlô oldalú háromszög két oldalát tesszük (3/b. ábra). Ezzel megnöveltük a szakasz hosszát az eredeti harmadával. Ezt az eljárást a végtelenségig folytathatjuk - de a 3/c. ábrán csak a következô lépés eredménye látható.
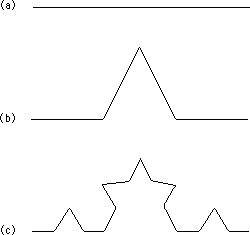
3. ábra: Koch-görbe, két lépés után.
(a) Egységszakasz. (b) A hossz 4/3-szorosára növekedett.
(c) A hossz megint 4/3-szorosára növekedett, azaz immár
az eredeti 16/9-ed szerese
Ezekben a példákban könnyû észrevenni az önhasonlóságot, de jóval bonyolultabb a dolog, ha áttérünk a nemlineáris fraktálokra, mint amilyen pl. a Mandelbrot-halmaz is.
Copyrights 1993, University of Illinois Board of Trustees
National Center for Supercomputing Applications, Education Group
rpanoff@ncsa.uiuc.edu és jgasaway@ncsa.uiuc.edu