Szepesváry Pál
Maxwellrõl és az õ eloszlásáról
Prológus
A világ megismerése – no, legyünk szerényebbek –, ismeretek megszerzése a világ megismeréséhez élményekkel jár. A megismerõ élénken emlékszik arra, ha hibát talált vagy talál, és annak több-kevesebb indulattal a végére is akar járni. Amikor azután errõl beszél, hol próbára teszi a hallgatóinak türelmét, hol kedvre deríti õket, de ártani aligha árt. Miért, miért nem, lélektanászok talán tudják vagy tudni vélik, bizonyos azonban az, hogy segít a tanulásban, ha valamely kemény anyagot a tanító személyes emlékeinek felidézésével színezi. Olyan ez, mint az idõs ember emlékirata. Legtöbbször van haszna. Legyen ez a mentsége az alább következõknek.
Maxwell eloszlásának tálalása
fél évszázada és most
A természettudományt lelkesen tanuló fiatal egyszer elér oda, hogy megtudja, a gázok molekulái szakadatlanul mozognak, méghozzá nem is lassan, melegben gyorsabban, hidegben kevéssé gyorsan. Azután azt is megtudja, hogy a kicsiny molekulák más sebességgel mozognak, mint a nehezebbek, amit nem is tart olyan hihetetlennek. Az azonban már furcsa, hogy ugyanannak a gáznak molekulái sem egyforma sebesen száguldoznak, hanem kis részük lassabban, ismét kis részük nagyon gyorsan, a szürke átlag pedig közepesen. De hát, ha ez a tapasztalat, biztosan így is van.
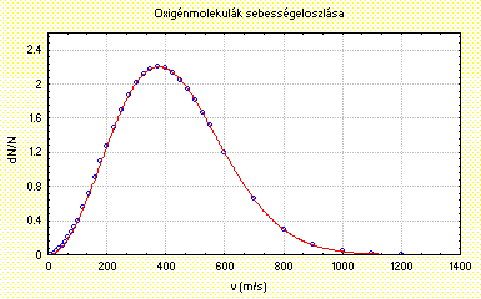
A természettudományt tanuló fiatal persze addigra tanult már elég fizikát ahhoz, hogy megszokja, a jelenségeket matematikai formába illik önteni. Nem lepi meg tehát, hogy tankönyvében talál egy "grafikont":

és a hozzátartozó magyarázatot. A szöveg pedig így hangzik: az ábra ordinátája megadja, hogy az összes molekulák hány százalékának sebessége egyenlõ az abszcisszán megadott értékkel. No de – okoskodik a tanuló –, ha az ábra és a magyarázat szerint szerint 400 m/s sebességgel mozog a molekulák kereken 2.2%-a, akkor nagyjából ennyi mozog 401 m/s sebességgel is, de a 400.5 m/s-mal, 400.25 m/s-mal, 400.75 m/s-mal haladók hányada is ennyi. Még 45 felezés és "1 méteren belül elfogyott a 100%". A bajért a tanuló elõször tanárát hibáztatja. Késõbb mentséget talál számára: bizonyára reménytelennek tartotta, hogy matematikában járatlan hallgatói megértsék a sûrûségfüggvények természetét, meg azt, hogy folytonos valószínûségi változónál nem kérdezünk rá konkrét értékének valószínûségére. Annyi járulékos baj azért az elnagyolással még járt, hogy a tanulók ezután mindenféle haranggörbét eloszlásfüggvénynek neveznek.
A mutatott rajz és az idézett szöveg ötvenéves. Emlék. Egy nagy hagyományú, jó hírû tudományos könyvkiadó ismeretterjesztõ sorozatának kémiai kötetében azonban napjainkban bukkan fel a következõ ábra:
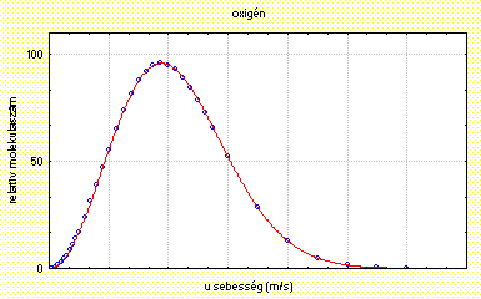
ami még kétségbeejtõbb lenne... ha a szövegben nem szerepelne az a megállapítás, hogy a Maxwell-féle sebességeloszlás azt adja meg: ...hány ...molekula található egy adott sebességintervallumban. És itt az intervallumon van a hangsúly. A mai tanulót már figyelmeztetik, hogy nem sebességekben, hanem sebességhatárokban kell gondolkodnia, de a függõleges tengely 0-tól 100-ig való beosztását ez sem menti. Az ábra úgy zavaró, ahogy van. Milyen sebességhatárhoz tartozik az a 100%?
Akkor hát mi van?
Mit mond Maxwell?
James Clerk Maxwell a sebességeloszlás kérdésérõl "Illustrations of the Dynamical Theory of Gases" címû dolgozatában értekezik, amely a Philosophical Magazine 19. és 20. évfolyamában jelent meg, a 19–32., ill. a 21–37. oldalakon 1858–1860 táján.
A dolgozat három részbõl áll. Az elsõ címe: "A tökéletesen rugalmas gömbök mozgásáról és ütközésérõl", a másodiké: "Két- vagy többféle mozgó részecske egymás közti diffúziójának folyamatáról", végül a harmadiké "Tetszõleges alakú, tökéletesen rugalmas testek ütközésérõl".
Az értekezés szép, rendszeres szerkezetû. Maxwell a válaszra váró kérdéseket, "propozíciók" alakjában fogalmazza meg. Fordíthatnánk a propozíciókat "tételeknek" is, de maradjunk a propozíciónál, mivel nem pusztán állításokról van szó. Egy-egy propozíció meghatározza a tárgyalt jelenséget, megadva annak feltételeit, és felteszi a szabatos kérdést. Erre következik azután a tárgyalás. A dolgozatban XXIII propozíció kerül sorra.
Témánkra nézve most az elsõ négy propozíció érdekes. Íme:
"I. propozíció. Két, ellentétes irányban mozgó, tömegükkel fordított arányban álló sebességû gömb összeütközik; meghatározandó mozgásuk az ütközés után.
Legyen P és Q a középpontok helyzete ütközéskor. AP, BQ a sebességek iránya és nagysága ütközés elôtt, Pa, Qb ugyanez ütközés után. Mármost felbontva a sebességeket a középpontok PQ vonalával párhuzamosan és arra merõlegesen, azt találjuk, hogy a középpontok vonalával párhuzamos sebességek pontosan fordítottak, míg a merõlegesek változatlanok. Összetéve újra ezeket a sebességeket, azt találjuk, hogy mindkét golyó sebessége ugyanaz ütközés elôtt és után, irányuk ütközés elôtt és után a középpontok vonalának síkjában fekszik és azzal egyezõ szöget zár be.
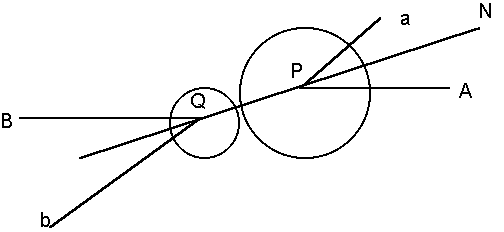
II. propozíció. Megtalálandó annak valószínûsége, hogy az ütközés utáni sebesség iránya adott határok közé esik.
Hogy egy ütközés megtörténhessék, az egyik golyó mozgásvonalának a másik központjához közelebb kell futnia, mint sugaraik összege; azaz át kell haladnia egy körön, amelynek középpontja a másik golyó középpontja, sugara (s) pedig a két golyó sugarának összege. Ezen a körön belül minden helyzet egyenlõ valószínûségû, ezért annak valószínûsége, hogy a középponttól számított távolság r és r + dr között legyen
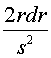
Ha most f az az APa szög, amelyet a eredeti és az ütközés utáni irányok bezárnak, akkor APN=½f, és r = s sin ½f , és a valószínûség:
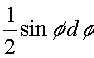
A f és f + df poláris távolságokhoz tartozó szögek által bezárt térrész
![]()
ennélfogva, haw az egységsugarú gömb felületének tetszõlegesen kicsiny felületrésze, akkor az ezen a felületen athaladó ütközési irány valószínûsége
![]()
tehát a valószínûség független f -tõl, azaz minden ütközési irány egyenlõen valószínû.
III. propozíció. Adott két gömb sebességének iránya és nagysága ütközés elôtt, a középpontok vonala ütközéskor; meghatározandók a sebességek ütközés után.
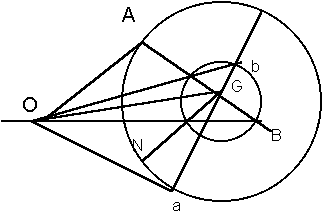
Jelölje OA és OB a sebességeket ütközés elôtt oly módon, hogy ha a testek nem hatnának egymásra, a másodperc végén A-ban, ill. B-ben lennének. Kössük össze A-t B-vel és legyen G súlypontjuk, az a pont, amelyet a közös hatás nem befolyásol. Rajzoljuk meg a GN vonalat, párhuzamosan az ütközéskori középponti vonallal (nem szükségképpen az AOB síkban). Az AGN síkban rajzoljuk meg az aGb vonalat, miáltal NGa = NGA, Ga =GA és Gb = GB. Ekkor az I. propozíció szerint Ga és Gb a G-re vonatkoztatott sebsségek lesznek. Ezt OG-vel összetéve Oa és Ob, az ütközés utáni valódi sebességek adódnak.
A II. propozíció szerint az aGb vonalnak minden iránya egyenlõen valószínû. Úgy tûnik tehát, hogy az ütközés utáni sebesség a súlypont sebességébõl és ama sebességbõl tevõdik össze, amely a gömbnek a súlyponthoz viszonyított, bármely irányban egyenlõ valószínûségû sebessége.
Ha egy tökéletesen rugalmas tartályban nagyszámú egyenlõ, gömb alakú részecske mozogna, azok ütköznének és sebességük minden ütközéskor változna; így egy bizonyos idõ múlva a vis viva bizonyos törvényszerûség szerint szétoszolna a részecskék között. A részecskék átlagos száma, amelyek sebessége bizonyos határok között van, megállapítható, bár egy-egy részecske sebessége minden ütközéskor megváltozik.
IV. propozíció. Meghatározandó azon részecskék átlagos száma, amelyek nagyszámú azonos részecskével való nagyszámú ütközés utáni sebessége bizonyos határok között van.
Legyen N a részecskék száma. Legyen x, y és z az egyes részecskék sebességének három komponense a három derékszögû irányban. Azon részecskék száma, amelyeknél x az x és x + dx határok közé esik legyen Nf(x)dx, ahol f(x) x-nek az a függvénye, amelyet meg kell határozni.
Azon részecskék száma, amelyeknél y az y és y + dy határok közé esik, Nf(y)dy lesz, azoké, amelyeknél z az z és z + dz határok közé esik, Nf(z)dz, ahol f mindig ugyanaz a függvény.
A x sebesség léte semminõ módon nem nem hat az y és z sebességekre, lévén ezek egymásra merõlegesek és függetlenek. Ennélfogva azoknak a részecskéknek száma, amelyek sebessége az x és x + dx , az y és y + dy és a z és z + dz határok között van
![]()
Ha feltesszük, hogy az N részecske ugyanabban a pillanatban indul a kezdõpontból, akkor ez a részecskék száma a (dx dy dz) térfogatelemben, és a részecskék száma egységnyi térfogatra vonatkoztatva
![]()
A koordináták iránya azonban teljességgel önkényes, minélfogva ez a szám csak a kezdõponttól mért távolságtól fog függeni
![]()
Ezt a függvényegyenletet megoldva az
![]()
eredményt kapjuk. Ha A-t pozitívnak tekintjük, a részecskék száma nõ a sebességgel, és a részecskék teljes száma végtelennek adódik. A-t ezért negatívnak és és –1/a2 értékûnek vesszük, ami miatt most a részecskék száma x és x + dx között
![]()
x = –¥ és x = +¥ között integrálva azt találjuk, hogy a részecskék teljes száma
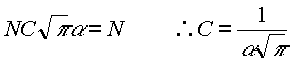
f(x) ennélfogva
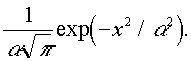
Mindezek alapján levonhatjuk az alábbi következtetéseket:
1. Azon részecskék száma, amelyek sebessége, bizonyos irányban felbontva, x és x + dx között van
(1) 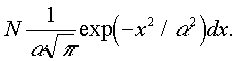
2. Azok száma, amelyek aktuális sebessége v és v + dv között van
(2) 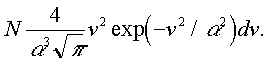
3. v sebesség átlagértékének megtalálására add össze minden részecske sebességét és oszd a részecskék számával. Az eredmény:
(3) 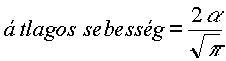
4. A v2 átlagértékének megtalálására add össze az értékekeket és ossz N-nel,
(4) 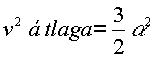
Ez nagyobb, mint az átlagsebesség négyzete, ahogyan ennek lennie is kell.
Ebbõl a propozícióból az látszik, hogy a sebességek a részecskék között ugyanúgy oszlanak meg, mint ahogyan a hibák oszlanak meg a megfigyeléseken a "legkisebb négyzetek módszerének" elméletében. A sebességek 0 és ¥ között változnak, de azok száma, amelyek sebessége nagy, viszonylag kicsi. A minden irányban egyenlõ sebességekhez hozzáadódhat a részecskék egész rendszerének általános transzlációs mozgása, amelyet össze kell tenni a részecskék egymáshoz viszonyított mozgásával. Az egyiket nevezhetjük transzlációs mozgásnak, a másikat keveredésnek."
Eddig Maxwell munkájának minket érdeklõ része. 1858-ban íródott. Maxwell ekkor 27 éves volt.
Pontosítsunk ezek után
Akár az ötven évvel ezelôtti tankönyv, akár a korszerû kézikönyv esetére gondolunk, a tárgyalás ellentmondásokra vezetõ elnagyolása annak eredménye, hogy a szerzõk ilyen vagy amolyan okból megkerülik a matematikai részleteket és ilyen vagy amolyan okból elhallgatják azokat a matematikai gondokat, amelyek a szóban forgó kérdés megoldása során felvetõdnek. A tárgyalt jelenséget rajzokkal szemléltetik, és egyik idézett példában sem szerepel "képlet", holott az feltehetõen segítene, mind abban, hogy a számolni lehessen, mind abban, hogy az alkalmazónak a gondolatmenetrõl tiszta képe legyen.
A szóban forgó kérdéshez, mint immár Maxwelltõl tudjuk, a
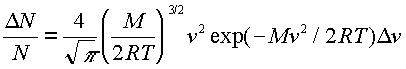
egyenlet tartozik, ahol a jelölések lényegében ismertek. Itt Maxwell (2) összefüggésének kissé bõvített változatáról van szó, az ott szereplõ a kapott részletesebb fizikai tartalmat. Az egyenlettel ismerkedõt változatlanul nyugtalaníthatja, dv avagy Dv áll a jobb oldalon, differenciálegyenletrõl van-e szó, egyáltalán mit keres a jobb oldal végén Dv? Az egyenlet most melyik függõleges tengelyének adatait adja meg? Ahány Dv, annyi függvény? És ez a formula most pontos, vagy közelítõ?
Ezek a kérdések tisztázhatók. Ismerjük fel, hogy a függvény, amelyet kerülgetünk, nem más, mint egy sûrûségfüggvény, annak összes tulajdonságával. Az
(2) 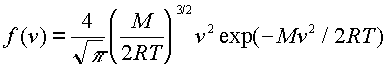
függvény az, amelynek v1 és v2 sebességek közötti határozott integrálásával szabatosan meg lehetne kapni a molekulák keresett, az adott sebességhatárok közé esõ valószínû hányadát.
A baj azonban az, hogy a (2) függvénynek nincs analitikusan megadható integrálja, más szóval, nincs olyan függvény, amelynek a (2) függvény lenne a primitív függvénye. Innen ered a sok nehézség, ezért nincsenek egyszerû "képleteink". Ha nincs analitikusan megadható integrálunk, numerikus módszerekhez folyamodunk. A legegyszerûbb az integrált téglalap területével közelíteni. Ez történik az (1) függvény esetében: a téglalap magassága a (2) függvény értéke valamely v-nél, alapja pedig Dv. Nem kétséges, amíg Dv nem nagyon széles, a pontosság nem rossz. A kérdés elvi, nem gyakorlati, de tudni érdemes, hogy ott közelítésrõl van szó. Egyébként, ha valakinek az (1) függvény, azaz a téglalap-területekkel való közelítés nem tetszik, választhat akármilyen más numerikus eljárást is.
Egy hasznos párhuzam
Hogy a Maxwell által levezetett (2) függvény sûrûségfüggvény, nyilvánvalóan nem véletlen. Amikor Maxwell azt írja, hogy a "részecskék átlagos száma, amelyek sebessége bizonyos határok között van, megállapítható, bár egy-egy részecske sebessége minden ütközéskor megváltozik", azt fejezi ki, amit a valószínûségszámítók a tömegjelenségek jellemzõ vonásának tanítanak. Természetes tehát, hogy Maxwell expressis verbis kijelentette, hogy valószínûségeket keres és éles elméjû következtetése, miszerint "a sebességek a részecskék között ugyanúgy oszlanak meg, mint ahogyan a hibák oszlanak meg a megfigyeléseken a 'legkisebb négyzetek módszerének' elméletében", rámutat a vizsgált folyamat statisztikus jellegére.
A véletlen hibákkal terhelt kísérleti eredmények kezelésében jelentõs szerepe van a különbözõ eltérések (pl. sok egyéb mellett a mért és számított értékek eltérése) négyzeteinek.és ezen négyzetek összegeinek. Ezekre vonatkozóan ismerte fel Karl Pearson 1900-ban a nevezetes c2-eloszlás – analitikusan persze megint nem integrálható – sûrûségfüggvényét:
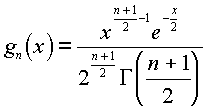 ha x > 0
ha x > 0
ahol a valószínûségi változó, amelyre ez a sûrûségfüggvény vonatkozik
![]()
négyzetösszeg, amelyben x változók függetlenek és egyforma, standard normális eloszlásúak. Rényi Alfréd emlékeztetett ismert tankönyvében arra, hogy a Pearson-függvény n = 3 esetén a
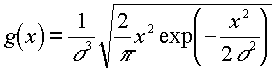
Maxvell-féle sebességeloszlás, ha x helyébe a v sebességvektornak, Maxwell munkájában x, y és z sebességkoordinátákkal kifejezett hosszát helyettesítjük:
![]()
ahol x, y és z független, azonos normális eloszlású változók. A gondolatmenetet megfordítva azt is mondhatjuk: ha a Pearson-eloszlás egyenértékû módon leírja a gázok kísérletben megfigyelt viselkedését, akkor a gázmolekulák sebessége pontosan feleljen meg a c2-eloszlás levezetésénél megkövetelt elõfeltételeknek.
Epilógus
Aki tanul, aki dolgozik, idõnkint megállapításokra bukkan, amelyekben kétségtelen hibát talál. Ez a hiba lehet jelentõs, lehet jelentéktelen. Olyan ez, mint egy nyelvi tévedés. Ha egy atomreaktor kiégett fûtõelemeit "reprocesszálni" kell, a latin nyelvben annyira, amennyire járatos ember fülét csak sérti ez a "processzura", és épp úgy szólni akar, mint a neves humorista, aki humorban nem ismeri a tréfát. Különösen teszi ezt akkor, ha a hiba elkövetõje erre, ilyen-olyan okból, még indulatilag is indítja.
Kérdés: érdemes-e? Érinti-e a felpattanás a lényeget? Hogy egy gáz egymással ütközõ, száguldó molekulák elegye, hogy a száguldás a gáz hõmérsékletének mértéke, ez lényeg. Hogy adott sebességû molekulák hányada leolvasható-e egy grafikonról, ez lényeg? Hogy kiégett fûtõelemeket újra fel kell dolgozni, ez lényeg. Hogy nem nyelvészeti szövegkörnyezetben kerékbe törjük a latin nyelvet, ez lényeg? Nem. És mégis, a pontosítás még soha nem ártott, tanulni lehet belõle. A szõrszálakat hasogatót pedig lehet szeretni, lehet rá haragudni, lehet legyinteni. Ez azonban lélektani kérdés, nem ismeretelméleti.
| Vissza az Elôadóba | http://www.kfki.hu/chemonet/ http://www.ch.bme.hu/chemonet/ |