Miért folyékony a higany?
Avagy miért nem kerülnek be a relativisztikus hatások a tankönyvekbe?

---

A fordítás Lars J. Norrby írása alapján készült (Why Is Mercury Liquid? Or, Why Do Relativistic Effects Not Get into Chemistry Textbooks?, Journal of Chemical Education, 1991. 68. k., 2. sz., 110–113. o.),  a JCE engedélyével. A Journal of Chemical Education lapjai a http://jchemed.chem.wisc.edu/ címen érhetõk el.

---

Már az ókorban is tudták, hogy a higany szobahõmérsékleten folyékony. Erre utal a görög eredetû hydrargyrum ("vizes ezüst") név (innen származik a Hg vegyjel) és a latin argentum vivum ("eleven ezüst") kifejezés, amely a német Quecksilber és az angol quicksilver névben él tovább. A másik angol név, a mercury és a francia mercure Mercuriusra, az istenek gyors lábú hírvivõjére utal.* Az alkimisták nagyon jól ismerték a higanyt – különösen fontosnak tartották, hogy az aranyat oldja. Az amalgamálás és az utána következõ hõbontás már Kr. e. 500 táján is a nemesfémek elõállítására szolgált a Földközi-tenger vidékén. Valószínûleg mindannyian ejtettünk már le hõmérõt és vadásztunk a szétguruló kis cseppek után. Szobahõmérsékleten a higany tehát folyékony. De miért? Ha megkérdezem a hallgatókat vagy a kollégákat, azt válaszolják "hát... mert... olyan alacsony az olvadáspontja". Ugyan!
 

Számos szervetlen kémiai tankönyvet és "bibliát" megnéztem, köztük a Greenwood–Earnshaw- (1) és a Cotton–Wilkinson-könyvet (2). A Mackay–Mackay-könyv (3) kivételével sehol sem találtam magyarázatot arra, hogy a higany folyékony. Az utóbbi szerzõk a "Relativisztikus hatások" címû részben térnek ki röviden a jelenségre. Cotton és Wilkinson néha említi ugyan a relativisztikus hatásokat, de nem tárgyalja, hogy milyen jelentõsen befolyásolják a kémiai tulajdonságokat. A Journal of Chemical Education ugyanakkor zavarba ejtõen sok cikket közöl errõl és a rokon problémákról (l. Pyykkö (4,5) és Javasolt irodalom). Ezek után felvetõdik a kérdés: miért nem került be ez a tudás a legfontosabb tankönyvekbe?

A következõkben összevetjük a kísérleti adatokat és az elméleti számításokat, majd a higanyban kialakuló kémiai kötéseket tárgyaljuk abban a reményben, hogy némi fényt derítsünk a szervetlen kémia néhány klasszikus kérdésére.
 

A higany és az arany
A két elem összehasonlítása nagyon érdekes, hiszen az arany és a higany "közvetlen szomszédok" a periódusos rendszerben, tulajdonságaik mégis eltérnek egymástól. Olvadáspontjaik például – az aranyé 1064 ^oC, a higanyé –39 ^oC – jobban különböznek, mint az összes többi szomszédos pár olvadáspontja (a Li–Be kivételével, ahol a különbség szintén 1100 ^oC körüli, de ennek más oka van). Sûrûségeik, az aranyé 19,32, a higanyé 13,53 gcm^–3, szintén jobban eltérnek, mint más elemek esetében. Olvadási entalpiák igen különbözõek; Au: 12,8, Hg: 2,30 kJmol^–1. Az olvadási entrópiák azonban hasonlóak; Au: 9,29, Hg: 9,81 JK^–1mol^–1, ami azt mutatja, hogy a Hg termodinamikai adatai "rendben vannak", hiszen egybehangzóan arra utalnak, hogy a kötõerõk sokkal gyengébbek a higanyban, mint az aranyban. Az adatok azt támasztják alá, amit már tudunk, de nem magyarázzák meg, miért folyékony a higany szobahõmérsékleten.

Az arany és a higany elektromos tulajdonságai igen különbözõek. Az arany kiváló vezetõ; vezetõképessége 426 kSm^–1, a higanyé csak 10,4 kS m^–1.  (Az itt szereplõ adatok a Greenwood–Earnshaw-könyvbõl (1) származnak, ha nem jelöljük külön a forrást.)

A szerkezeteket összevetve megjegyezzük, hogy a Cu, Ag és Au köbös, a Zn és Cd (kissé torzított) hexagonális, szoros illeszkedésû kristályokat képez. A Hg azonban romboéderesen torzult, és a Hg–Hg távolság a nem egészen szoros illeszkedésû síkokban kb. 16%-kal nagyobb "a kelleténél". Ismét azt látjuk, hogy a higanyban a fém–fém kötés gyengébb  "az elvártnál".

Bár az arany és a higany elektronszerkezete nagyon hasonló,

₇₉Au(g):₅₄Xe|4f¹⁴,5d¹⁰,6s¹
₈₀Hg(g):₅₄Xe|4f¹⁴,5d¹⁰,6s²

számíthatunk rá, hogy ez a kis különbség okozhatja a meglepõen eltérõ tulajdonságokat. De hogyan?

Anomáliák
A ritkaföldfémek utáni elemeket nézve számos váratlan periodikus tulajdonságot találunk. Jól ismert példa a Hf és a Zr meglepõ hasonlósága. Ezt általában a lantanidakontrakcióval magyarázzák, amelyet a 4f héj betöltõdése okoz. A 4f elektronok nem árnyékolják olyan jól a magtöltést, mint az s, p vagy akár a d elektronok. Ez egyre nagyobb effektív magtöltéshez és ennek megfelelõen az elektronfelhõ összehúzódásához vezet. Valószínûleg jórészt ennek köszönhetõ, hogy a ₇₁Lu³⁺ körülbelül 0,03 Ã-mel kisebb, mint a ₃₉Y³⁺, noha a lutéciumionban 32-vel több elektron van. Ugyancsak a lantanidakontrakcióval magyarázzák az ezüst és az arany, illetve a kadmium és a higany azonos ionsugarát.

Miért aranyszínû az arany? Miért nem ezüstszínû? Miért az arany a legnagyobb elektronaffinitású elem a valóban elektronegatív elemeket leszámítva?  Az arany elektronaffinitása –223 kJmol^–1; nagyobb, mint a kéné és majdnem akkora, mint a jódé. Minek tulajdonítható, hogy a Tl a +1-es, az Pb a +2-es, a Bi a +3-as oxidációs állapotban stabil, míg rokonaik rendre a +3-as, +4-es és a +5-ös állapotban stabilak?

A lantanidakontrakció elve – bármennyire hasznos – nem magyaráz meg minden anomáliát. Elõfordul, hogy az "iners 6s² pár"-ra hivatkoznak, amelyet Sidgwick vezetett be 1933-ban (l. pl. a klasszikus Phillips–Williams-könyvet (6)). Ez utóbbi elgondolás sem magyarázza azonban meg, miért folyékony a higany, és az Pb(II) miért stabilabb az Pb(IV)-nél. Ezeknek a jelenségeknek az értelmezéséhez a relativitáselméletet kell segítségül hívnunk.

Relativisztikus hatások
Einstein speciális relativitáselmélete szerint minden mozgó tárgy tömege nõ a sebesség függvényében:

Bohr kiszámította, hogy a hidrogénatomban az 1s elektron sebessége alapállapotban a fénysebesség 1/137-e, ha az elektron a Bohr-sugár távolságában kering. Ez a sebesség olyan kicsi, hogy a relativisztikus tömeg csak a nyugalmi tömeg 1,00003-szorosa. (Sommerfeld a kis relativisztikus hatásokat is figyelembe vette, amikor  a Bohr-modellt finomítva elliptikus pályákat vezetett be.) Egy hidrogénnél nehezebb atomban egy 1s elektron várható átlagos radiális sebessége

Ha a ₈₀Hg-t tekintjük, (80/137)·c=0,58c, vagyis a várható átlagos radiális sebesség a fénysebesség 58%-a, s a relativisztikus tömeg a nyugalmi tömeg 1,23-szorosa lesz. Ez azt jelenti, hogy a Bohr-sugár 23%-kal csökken, mert az elektron tömege a nevezõben szerepel. Tehát az arany és a higany 1s pályái jelentõsen összehúzódnak. Miután a pályának ortogonálisnak kell lenniük egymásra, csaknem azonos nagyságú kontrakció alakul ki a 2s, 3s, 4s, 5s, 6s és 7s pályák esetében is.

Nézzük most a kvantummechanikai hatásokat. Az elektronspint két holland fizikus, Uhlenbeck és Goudsmit "találta fel" 1925-ben a hidrogénspektrum finomszerkezetének értelmezésére. Az elmélet bizonyítékaként az 1922-ben elvégzett Stern–Gerlach-kísérletet tekintették (az elpárologtatott ezüstatomokból álló sugár kettévált az inhomogén külsõ mágneses tér hatására). Talán érdekes, hogy Pauli, aki 1925 elején bevezette a negyedik kvantumszámot, nem értett egyet azzal, hogy Uhlenbeck és Goudsmit az elektron természetébõl eredõ mozgásnak tekintette a spint. A kvantummechanika  és a relativitáselmélet szintézisét Dirac teremtette meg 1928-ban. Õ mutatta ki, hogy a spin–pálya csatolás relativisztikus hatás, minden elektronnak impulzusmomentuma van és nincs különbség a "pálya" és a "spin" impulzusmomentum között. Az impulzusmomentum kvantumszám, j egyetlen mennyiséget jelöl. Az s pályát s_1/2 jellemzi. Az "elektronspin" spektroszkópiai mérésekben ez az impulzusmomentum játszik szerepet. A Dirac-elméletbõl az is következik, hogy a p_x, p_y és p_z pályák nagyon különböznek szokásos felfogásunktól. A p_1/2-del és a p_3/2-del jellemzett pályák csoportjába sorolhatók, s mindkét típushoz a j kvantumszám rendelhetõ. A p_1/2 gömbszimmetrikus, és a fánk alakú p_3/2 pályánál kisebb energiájú. Dirac szerint a pályaenergiák relativisztikus felhasadása magyarázza a spin–pálya csatolási energiát. Ez a nehéz elemek, például az ólom esetében 2 eV (vagy közel 200 kJ mol^–1) is lehet.

Végsõ soron három relativisztikus hatásról beszélhetünk:
az s_1/2 és a p_1/2 pálya jelentõsen, a p_3/2 kisebb mértékben húzódik össze;
ennek hatására a d és f pályák – az s és p pályákhoz képest – kiterjednek;
a spin–pálya csatolás a p, d és f pályaenergiák relativisztikus felhasadása, az effektus a nehezebb elemek esetében nagy.

Ezeknek a hatásoknak az összessége igen fontossá válik az arany és a higany esetében, mert az 5d_5/2 és a 6s_1/2 pályák közötti energiakülönbséget csökkenti. Legalább még egy relativisztikus hatást figyelembe kell venni, a Darwin-járulékot, amely az elektron rezgõmozgását veszi számításba (ez az atommag közelében jelentõs). Hatására az s elektron energiája megnõ, az s pályák tágulnak, ami csökkenti a kontrakciót.

Relativisztikus számítások
Az arany és más nehézfémek relativisztikus energia-sávszerkezetét többféle módon is kiszámolták (4, 5, 7, 8). Ezek bemutatása nem könnyû a jelen cikk keretei között. A számunkra legfontosabb eredményeket az 1. ábra illusztrálja az AgH(g) és az AuH(g) molekulák esetében (9, 10). Az ezüst 4d és 5s pályáinak, valamint az arany 5d és 6s pályáinak különbsége igen eltérõ, bár nem relativisztikus megfelelõik hasonlóak. A gáz halmazállapotú szabad aranyatom, az AuH(g) molekula és a kristályos szilárd anyag  természetesen különbözik egymástól, de a relativisztikus hatások legfontosabb jellemzõi hasonlóak (8, 11). Schwerdtfeger és munkatársai az arany kémiájában megmutatkozó relativisztikus hatásokról írtak kitûnõ dolgozatokat (12, 13). Takeuchi és munkatársainak számításai szerint (14) relativisztikus effektusnak tulajdonítható, hogy az arany kohéziós energiája nagyobb az ezüsténél.

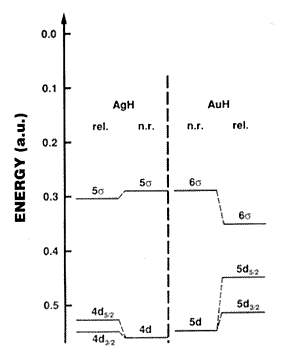
1. ábra. Az AgH(g) és az AuH(g) kétatomos molekula pályaenergiái a relativisztikus és a nem relativisztikus számítások alapján. (Az energia atomi egységekben (a.u.) van feltüntetve,1 a.u. = 27,212 eV = 2625,5 kJ mol^–1.) Tehát a függõleges tengelyen DE » 260 kJ felel meg egy osztásköznek. Pyykkö (9) nyomán.

Az arannyal és más nehézfémekkel végzett röntgen-fotoelektron sepktroszkópiai (ESCA) vizsgálatok azt mutatják, hogy a relativisztikus számítások eredményei jobban egyeznek a kísérlettel, mint a nem relativisztikus eredmények. A mérések és a számítások egyaránt arra utalnak, hogy a szilárd aranyban a fém-fém kötéseket a 6s és az 5d elektronok hozzák létre szinte a 6p elektronok nélkül.

Említésre méltó, hogy a relativiszitikus effektusok nem egyenletesen változnak a rendszám függvényében. A ₇₉Au-nál tûnnek a legnagyobbnak. A szabad Au(g) atom 6s pályájának relativisztikus kontrakciója, amely a tömeg sebességfüggésébõl származik kb. 16% (8). Ehhez hozzáadódik a lantanidakontrakció (amelyben szintén szerepet játszanak relativisztikus hatások), továbbá az 5d pályák hasonló összehúzódása. A szilárd aranyban a 6s elektron 2,8 eV (270 kJ mol^–1) teljes stabilizációs energiája 2/3 részben származik relativisztikus hatásokból és 1/3 részben lantanidakontrakcióból (15, 16). Ezeknek a hatásoknak eredménye általában nehezen jósolható meg.

Az ezüst és az arany
Most már számos különbséget megmagyarázhatunk. Az arany színe annak köszönhetõ, hogy a fém kék fényt elnyeli és az 5d elektronok a 6s szintre, pontosabban a Fermi-szintre gerjesztõdnek, amely a vezetési sáv tetején helyezkedik el. Az ezüst energiasávjai azonban távolabb vannak, ezért az elem UV-fényt nyel el, és színtelennek látszik. Az arany elsõ ionizációs energiája kissé nagyobb, mint az ezüsté, míg a második és a harmadik ionizációs energia az ezüst esetében nagyobb. Ezért gyakrabban találkozunk Ag(I)-, mint Au(I)-vegyülettel, de az Au(III)-vegyületek gyakoribbak az Ag(III)-nál. Ezenkívül az arany kötései jobban megközelítik a kovalens jelleget a komplexekben; ez a d–s hibrid pályáknak köszönhetõ, amelyek energetikailag kedvezõbbek, mint az ezüstben. Az 1. ábra mindezzel kvalitatív egyezést mutat (17).

Az elektronaffinitás
Az arany nagy elektronaffinitását a következõképpen magyarázhatjuk. A 6s pálya energiája olyan alacsony, hogy egy külsõ elektron könnyen a pályára ugorhat. A relativisztikus hatások az arany elektronaffinitását 65%-kal növelhetik meg (18). Ugyancsak relativisztikus hatások magyarázzák az Au₂(g) molekula meglepõ stabilitását. A molekula disszociációs energiája (221 kJmol^–1) nagyobb, mint a I₂(g)-é (151 kJmol^–1) és alig kisebb, mint a Cl₂(g)-é (243 kJmol^–1).

Intermetallikus vegyületek
A CsAu nem fémesen vezetõ ötvözet, hanem vörös, átlátszó, CsCl-szerkezetben kristályosodó félvezetõ. Ez szintén arra utal, hogy az Au 6s pályájára könyen beléphet még egy elektron. A kísérleti adatok a 2.ábrán láthatók (19). A CsAu elektronszerkezétnek számítása alátámasztja (19), hogy a félvezetõ jelleg relativisztikus hatásnak tudható be. Az arany itt nem különbözik teljesen a jódtól, ezért "pszeudohalogénnek" is nevezik.

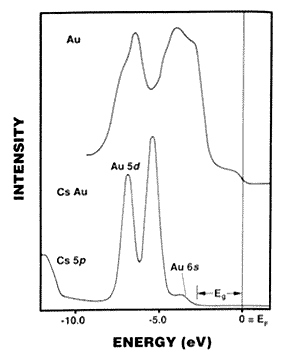
2. ábra. Az arany és a félvezetõ CsAu ESCA- (XPS-) spektruma. Az eV-ban megadott energiaértékek az E_F Fermi-szintre vonatkoznak. Az aranyban a 6s és az 5d sáv összeolvad (hibridizálódik) és a Fermi-szintig húzódik. A CsAu-ban az elektronsûrûség a Cs-ról az Au-ra tolódik át. A 6s sáv most lokalizált, nem keveredik az 5d sávval, és a Fermi-szinttõl E_g » 2,6 eV energiasáv választja el. Az Au 5d energiáinak kb. 1,5 eV-os relativisztikus felhasadása jól érzékelhetõ a CsAu esetén. Wertheim (19) nyomán.

Miért folyékony a higany?
A válaszhoz a gázfázist és a Hg(I)-et kell megvizsgálnunk. A higany nem képez kovalens egyszeres kötést, mint az Au₂.  Az Au₂-vel azonos számú elektront tartalmazó H₂²⁺ azonban nagyon stabil; vizes oldatban  és szilárd vegyületekben is elõfordul. A számítások szerint (21) a relativisztikus effektusok mind az Au₂-ben, mind a H₂²⁺-ben 16%-kal csökkentik a kötéshosszakat, s így a kötések rövidebbek, mint az analóg réz- és kadmiumvegyületekben. Ha párhuzamot akarunk vonni, azt mondhatjuk, hogy olyan különbség van a stabil Au₂(g) molekulát alkotó arany és a higany között, amely a gázfázisban a fémek közül egyedül létezik szinte kizárólag monomerként, Hg(g) alakban, mint a H₂(g) és a szigorúan monomer He(g) között. A szokásos magyarázat szerint azért nincs He₂(g), mert a harmadik és negyedik vegyértékelektron a nemkötõ 1s* pályát töltené be, tehát elbontaná a kétatomos molekulát. A Hg-ban a relativisztikusan összehúzódott 6 s pálya be van töltve, ezért a két 6s elektron kis járulékot ad a fém-fém kötéshez. Éppen az ellenkezõje igaz az arany esetében. Tehát a higanyban a  Hg–Hg-kötés elsõsorban van der Waals-erõknek (22) és talán a 6p pályák gyenge kölcsönhatásának köszönhetõ, ezért gyenge.

Most arra is magyarázatot kapunk, hogy miért sokkal rosszabb vezetõ a higany az aranynál: a két 6s elektron igen lokalizált, s csak kis járulékot szolgáltat a vezetési sávhoz. Ennek az analógiának az alapján a higanyt pszeudonemesgáznak is nevezhetnénk.

Amalgámozás
Miért oldja a folyékony higany az aranyat és miért képez amalgámot? Milyen a kémiai kötés az amalgámban? Miért alkot a higany amalgámot a rézzel, az arannyal, az ezüsttel és az alkálifémekkel? Miért reagál az ammóniumgyökkel? Miért reagál alig vagy miért nem reagál az átmeneti fémek többségével? Már említettük, hogy az arany hevítéssel kinyerhetõ az amalgámból, tehát a Hg és az Au közötti kötés nem erõs. Tekintsünk egy képzeletbeli gázalakú molekulát, a HgAu(g)-t. A spektroszkópiai úton elemzett He₂⁺-hoz hasonlóan háromelektronos kötése lenne (Hg···Au), két elektron a kötõ 6s, egy a nemkötõ 6s* pályán helyezkedne el. Ez a kötés gyengébb lenne, mint az Au₂(g) egyszeres kötése, de erõsebb, mint a Hg-atomok közötti kötés. Az ezüst és az arany atomonként egy elektront ad az amalgámkötésbe. Ugyanez érvényes az alkálifémekre. A legtöbb átmeneti fém azért reagál gyengén a higannyal, mert atomonként két s elektronnal járul hozzá a kötéshez, de ekkor a tiszta higany esetéhez jutunk vissza: csak nagyon gyenge kötések alakulhatnak ki. Úgy tûnik, hogy ha az ötvözõ fém egy elektront ad atomonként, jó amalgám képzõdik.

Hangsúlyozni kell, hogy a fentieket nem támasztják alá egyértelmû számítások. A szilárd higany kötési sávjának relativisztikus számításához rendszerint fel kell tételezni, hogy a fém kristályszerkezete vagy szoros illeszkedésû köbös, vagy köbös tércentrált. A kristályos higany romboéderes torzulása miatt a köbös tércentrált elrendezés rossz közelítés lenne. Az Au–Hg biner rendszerben nem találtak olyan intermetallikus fázist, amely több higanyt tartalmazna, mint az Au₂Hg. Ennek a sztöchiometrikus vegyületnek hexagonális kristályszerkezete van, amely 122 ^oC-on olvad inkongruensen. Az arany a szilárd higanyban szinte oldhatatlan (23). A nagy higanytartalmú amalgámok ezért többé-kevésbé az Au₂Hg és a Hg jól kristályosodó, kétfázisú keverékei. Ugyancsak hasznosak lennének a folyékony higanyon végzett relativisztikus számítások, amelyek a folyadék szerkezetét (a nyolc közeli szomszédból álló egységeket) is figyelembe vennék.

Az iners 6s² pár
Utolsó példaként hasonlítsuk össze a ₈₁Tl-t és a ₄₉In-t. Bár a Tl⁺-ion sugara nagyobb (1,50 Ã), mint az In⁺-é (1,40 Ã), a Tl⁺ nagyobb energia árán juthat a +1-es oxidációs állapotból a +3-asba, mint az In⁺. A második és a harmadik ionizációs energia összege a Tl esetében 4848  kJmol^–1, az In-nál 4524  kJmol^–1, a különbség kb. 7%. A Tl⁺-ionban ugyanannyi elektron van, mint a Hg-ban. A Tl³⁺-ion képzõdésekor a két elektron eltávolításához szükséges energiatöbblet nyilvánvalóan a 6s pálya relativisztikus kontrakciójából származik. A tankönyvekben gyakran szereplõ "iners 6s² pár"-ról mégsem írják, hogy relativisztikus effektus eredménye.

Legalább 15 éve ismert, hogy a relativisztikus hatások befolyásolják a nehéz elemek tulajdonságait. Ezt a tudást a kutatók felhasználják munkájuk során (24–26). Itt az ideje, hogy az egyetemi kémiatanításban is szó essen róla.

---

Javasolt irodalom
Pitzer, K. S. Acc. Chem. Res. 1979, 12, 271.
Pyykkö, P.; Desclaux, J. P. Acc. Chem. Res. 1979, 12, 276.
Malli, G. L., Ed. Relativistic Effects in Atoms, Molecules, and Solids; Plenum: New York, 1983.
Christensen, N. E. Int. J. Quant. Chem. 1984, 25, 223.
Christiansen, P. A.; Ermler, W. C.; Pitzer, K. S. Ann. Rev. Phys. Chem. 1985, 36, 407.
Pyykkö, P. Chem. Rev. 1988, 88, 563.

A Journal of Chemical Education cikkei
Powell, R. E. J. Chem. Educ. 1968, 95, 558.
Szabo, A. J. Chem. Educ. 1969, 46, 678.
McKelvey, D. R. J. Chem. Educ. 1983, 60, 112.
Banna, M. S. J. Chem. Educ. 1985, 62, 197.
Mason, J. J. Chem. Educ. 1988, 65, 17.

Idézett irodalom
1. Greenwood, N. N.; Earnshaw, A. Chemistry of the Elements; Pergamon: Oxford, 1984; p 1395.
2. Cotton, F. A.; Wilkinson, G. Advanced Inorganic Chemistry, 5th ed.; Wiley: New York, 1988; p 597.
3. Mackay, K: M.; Mackay; R. A. Introduction to Modern Inorganic Chemistry, 4th ed.; Blackie: Glasgow and London; 1989; p 292.
4. Pyykkö, P. Relativistic Theory of Atoms and Molecules, A Bibiography 1916-1985; Springer: Berlin;.1986. Több mint 3100 hivatkozást tartalmaz!
5. Pyykkö, P. Chem. Rev: 1988; 88, 563.
6. Phillips, C. S. G.; Williams, R. J. P. Inorganic Chemistry; Oxford University: New York, 1966; Vol. 2, Metals.
7. Takeda, T. J: Phys. F.: Metal Phys. 1980, 10, 1135.
8. Christensen; N. E. Int. J. Quant. Chem. 1984; 25, 233.
9. Pyykkö, P. Adv. Quant. Chem. 1978. 11, 353.
10. Pyykkö, P; Desclaux; J. P. Acc. Chem. Res. 1979, 12, 276.
11. Koelling; D. D.; MacDonald, A. H. In Relativistic Effeets in Atoms, Molecules, and Solids; Malli,.G. L.; Ed.; Plenum: New York, 1983; p 227.
12. Schwerdtfeger; P., Dolg, M.; Schwarz, W. H. E.; Bowmaker, G. A.; Boyd, P. D. W. J. Chem. Phys. 1989, 91,1762.
13. Schwerdtfeger, P. J. Am. Chem. Soc. 1989, 111, 7261.
14. Takeuchi, N.; Chan, C. T.; Ho, K. M. Phys. Rev. B. 1989, 40, 1565.
15. Bagus, P. S.; Lee, Y. S.; Pitzer, K. S.. Chem. Phys. Lett. 1975, 33, 408.
16. Christiarisen, P. A.; Ermler, W. C.; Pitzer, K. S. Ann. Rev. Phys. Chem. 1985, 36, 407.
17. Desclaux, J. P.; Pyykkö, P. Chem. Phys. Lett. 1976, 300.
18. Cole, L. A.; Perdew, J. P. Phys. Rev. A 1982, 25, 1265.
19. Wertheim, G. K. In Solid State Chemistry Techniques; Cheetham, A. K.; Day, P., Eds.; Clarendon: Oxford, 1987, Chapter 3.
20. Christensen, N. E.; Kollar, J. Sol. State Comm. 1983, 46, 727.
21. Ziegler, T.; Snijders, J. G.; Baerends, E. J. J. Chem. Phys. 1981, 74, 1271.
22. Pyper, N. C.; Grant, I. P.; Gerber, R. B. Chem. Phys. Lett. 1977, 99. 479.
23. Rolfe, C.; Hume-Rothery, W. J. Less Comm. Met. 1967, 13, 1.
24. Gillespie, R. J.; Granger, P., Morgan, K. R.; Schrobilgen, G. J. Inorg. Chem. 1984, 23, 88 7.
25. Burns, R. C.; Devereaux, L. A., Granger, P.; Schrobilgen, G. J. Inorg. Chem. 1985, 24, 2615.
26. Björgvinsson; M.; Sawyer, J. F.; Schrobilgen, G. J. Inorg. Chem. 1987, 26, 741.